From Förberedande kurs i matematik 1

Revision as of 09:56, 9 September 2008 (edit) Tekbot (Talk | contribs) m (Lösning 4.3:5 moved to Solution 4.3:5: Robot: moved page) ← Previous diff		Current revision (14:33, 9 October 2008) (edit) (undo) Tek (Talk | contribs) m
(One intermediate revision not shown.)
Line 1:		Line 1:
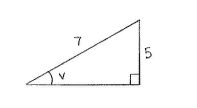
-	{{NAVCONTENT_START}}	+	An often-used technique to calculate <math>\cos v</math> and <math>\tan v</math>, given the sine value of an acute angle, is to draw the angle <math>v</math> in a right-angled triangle which has two sides arranged so that <math>\sin v = 5/7\,</math>.
-	<center> [[Image:4_3_5-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
-	{{NAVCONTENT_START}}	+
-	<center> [[Image:4_3_5-2(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
	[[Image:4_3_5_1.gif|center]]		[[Image:4_3_5_1.gif|center]]
-	[[Image:4_3_5_2.gif|center]]	+
		+	Using the Pythagorean theorem, we can determine the length of the third side in the triangle.
		+
		+	{| align="center"
		+	||[[Image:4_3_5_2.gif]]
		+	||<math>\begin{align}&x^2 + 5^2 = 7^2\\[5pt] &\text{which gives that}\\[5pt] &x = \sqrt{7^2-5^2} = \sqrt{24} = 2\sqrt{6}\end{align}</math>
		+	|}
		+
		+	Then, using the definition of cosine and tangent,
		+
		+	{{Displayed math||<math>\begin{align}
		+	\cos v &= \frac{x}{7} = \frac{2\sqrt{6}}{7}\,,\\[5pt]
		+	\tan v &= \frac{5}{x} = \frac{5}{2\sqrt{6}}\,\textrm{.}
		+	\end{align}</math>}}
		+
		+
		+	Note: The right-angled triangle that we use is just a tool and has nothing to do with the triangle that is referred to in the question.

---

Current revision

An often-used technique to calculate \displaystyle \cos v and \displaystyle \tan v, given the sine value of an acute angle, is to draw the angle \displaystyle v in a right-angled triangle which has two sides arranged so that \displaystyle \sin v = 5/7\,.

Using the Pythagorean theorem, we can determine the length of the third side in the triangle.

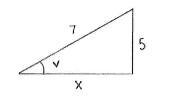
\displaystyle \begin{align}&x^2 + 5^2 = 7^2\\[5pt] &\text{which gives that}\\[5pt] &x = \sqrt{7^2-5^2} = \sqrt{24} = 2\sqrt{6}\end{align}

Then, using the definition of cosine and tangent,

\displaystyle \begin{align} \cos v &= \frac{x}{7} = \frac{2\sqrt{6}}{7}\,,\\[5pt] \tan v &= \frac{5}{x} = \frac{5}{2\sqrt{6}}\,\textrm{.} \end{align}

Note: The right-angled triangle that we use is just a tool and has nothing to do with the triangle that is referred to in the question.