Solution 2.3:9b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 2.3:9b moved to Solution 2.3:9b: Robot: moved page)
Current revision (14:11, 29 September 2008) (edit) (undo)
m
 
(One intermediate revision not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The points of intersection are those points on the curve which also lie on the ''x''-axis, i.e. they are those points which satisfy both the equation of the curve
-
<center> [[Image:2_3_9b-1(2).gif]] </center>
+
<math>y=x^{2}-5x+6</math> and the equation of the ''x''-axis <math>y=0</math>,
-
{{NAVCONTENT_STOP}}
+
 
-
{{NAVCONTENT_START}}
+
{{Displayed math||<math>\left\{\begin{align}
-
<center> [[Image:2_3_9b-2(2).gif]] </center>
+
y&=x^{2}-5x+6\,,\\
-
{{NAVCONTENT_STOP}}
+
y&=0\,\textrm{.}
 +
\end{align}\right.</math>}}
 +
 
 +
This system of equations gives directly that <math>y=0</math> and that <math>x</math> must satisfy the quadratic equation <math>x^{2}-5x+6=0\,</math>. By completing the square, we obtain that the left-hand side is
 +
 
 +
{{Displayed math||<math>\begin{align}
 +
x^{2} - 5x + 6 &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \Bigl(\frac{5}{2}\Bigr)^{2} + 6\\[5pt]
 +
&= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{25}{4} + \frac{24}{4}\\[5pt]
 +
&= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{1}{4}
 +
\end{align}</math>}}
 +
 
 +
and this gives that the equation has solutions <math>x=\tfrac{5}{2}\pm\tfrac{1}{2}</math>, i.e. <math>x=\tfrac{5}{2}-\tfrac{1}{2}=\tfrac{4}{2}=2</math> and <math>x=\tfrac{5}{2}+\tfrac{1}{2}=\tfrac{6}{2}=3</math>.
 +
 
 +
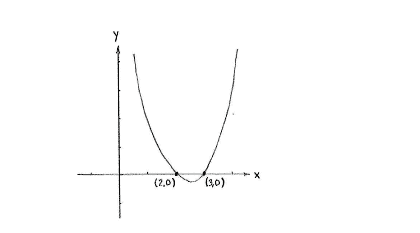
The intersection points are therefore (2,0) and (3,0).
 +
 
 +
 
 +
<center>[[Image:2_3_9b-2(2).gif]]</center>

Current revision

The points of intersection are those points on the curve which also lie on the x-axis, i.e. they are those points which satisfy both the equation of the curve \displaystyle y=x^{2}-5x+6 and the equation of the x-axis \displaystyle y=0,

\displaystyle \left\{\begin{align}

y&=x^{2}-5x+6\,,\\ y&=0\,\textrm{.} \end{align}\right.

This system of equations gives directly that \displaystyle y=0 and that \displaystyle x must satisfy the quadratic equation \displaystyle x^{2}-5x+6=0\,. By completing the square, we obtain that the left-hand side is

\displaystyle \begin{align}

x^{2} - 5x + 6 &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \Bigl(\frac{5}{2}\Bigr)^{2} + 6\\[5pt] &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{25}{4} + \frac{24}{4}\\[5pt] &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{1}{4} \end{align}

and this gives that the equation has solutions \displaystyle x=\tfrac{5}{2}\pm\tfrac{1}{2}, i.e. \displaystyle x=\tfrac{5}{2}-\tfrac{1}{2}=\tfrac{4}{2}=2 and \displaystyle x=\tfrac{5}{2}+\tfrac{1}{2}=\tfrac{6}{2}=3.

The intersection points are therefore (2,0) and (3,0).


Image:2_3_9b-2(2).gif
Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_2.3:9b"