From Förberedande kurs i matematik 1

Revision as of 08:53, 9 September 2008 (edit) Tekbot (Talk | contribs) m (Lösning 2.3:10a moved to Solution 2.3:10a: Robot: moved page) ← Previous diff		Current revision (14:25, 29 September 2008) (edit) (undo) Tek (Talk | contribs) m
(One intermediate revision not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	Individually, the inequalities <math>y\ge x^{2}</math> and <math>y\le 1</math> define the region above the parabola <math>y=x^{2}</math> and under the line <math>y=1</math>, respectively.
-	<center> [[Image:2_3_10a.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{| align="center"
-	[[Image:2_3_10_a.gif|center]]	+	|align="center"|[[Image:2_3_10_a-1.gif|center]]
		+	|width="10px"|&nbsp;
		+	|align="center"|[[Image:2_3_10_a-2.gif|center]]
		+	|-
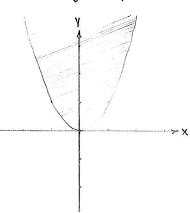
		+	|align="center"|<small>The region ''y''&nbsp;≥&nbsp;''x''²</small>
		+	||
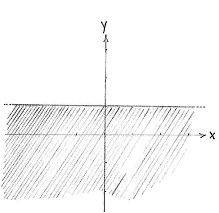
		+	|align="center"|<small>The region ''y''&nbsp;≤&nbsp;1</small>
		+	|}
		+
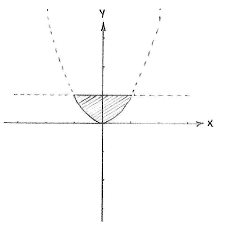
		+	Those points which satisfy both inequalities lie in the region above the parabola, but below the line <math>y=1\,</math>.
		+
		+
	[[Image:2_3_10_a2.gif|center]]		[[Image:2_3_10_a2.gif|center]]

---

Current revision

Individually, the inequalities \displaystyle y\ge x^{2} and \displaystyle y\le 1 define the region above the parabola \displaystyle y=x^{2} and under the line \displaystyle y=1, respectively.

The region y ≥ x²		The region y ≤ 1

Those points which satisfy both inequalities lie in the region above the parabola, but below the line \displaystyle y=1\,.