From Förberedande kurs i matematik 1

Revision as of 08:47, 9 September 2008 (edit) Tekbot (Talk | contribs) m (Lösning 2.2:5c moved to Solution 2.2:5c: Robot: moved page) ← Previous diff		Current revision (12:34, 24 September 2008) (edit) (undo) Tek (Talk | contribs) m
(One intermediate revision not shown.)
Line 1:		Line 1:
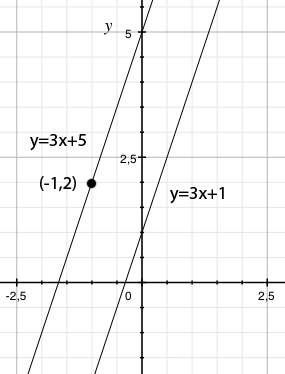
-	{{NAVCONTENT_START}}	+	Two straight lines are parallel if they have the same slope. From the line
-	[[Image:S1_2_2_5_c.jpg]]	+	<math>y=3x+1</math>, we can read off that it has a slope of 3 (the coefficient in front of ''x''), and hence the equation we are looking for has an equation of the form
-	<!--<center> [[Image:2_2_5c.png]] </center>-->	+
-	{{NAVCONTENT_STOP}}	+	{{Displayed math||<math>y=3x+m\,,</math>}}
		+
		+	where ''m'' is a constant. The condition that the line should also contain the point (-1,2) means that the point should satisfy the equation of the line
		+
		+	{{Displayed math||<math>2=3\cdot (-1)+m\,,</math>}}
		+
		+	which gives <math>m=5</math>. Hence, the equation of the line is <math>y=3x+5</math>.
		+
		+
		+	<center>[[Image:S1_2_2_5_c.jpg]]</center>

---

Current revision

Two straight lines are parallel if they have the same slope. From the line \displaystyle y=3x+1, we can read off that it has a slope of 3 (the coefficient in front of x), and hence the equation we are looking for has an equation of the form

\displaystyle y=3x+m\,,

where m is a constant. The condition that the line should also contain the point (-1,2) means that the point should satisfy the equation of the line

\displaystyle 2=3\cdot (-1)+m\,,

which gives \displaystyle m=5. Hence, the equation of the line is \displaystyle y=3x+5.