Solution 4.1:7c
From Förberedande kurs i matematik 1
(Difference between revisions)
m |
|||
| (3 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
| - | + | By completing the square, we can rewrite the ''x''- and ''y''-terms as quadratic expressions, | |
| - | < | + | {{Displayed math||<math>\begin{align} |
| + | x^2 - 2x &= (x-1)^2 - 1^2\,,\\[5pt] | ||
| + | y^2 + 6y &= (y+3)^2 - 3^2\,, | ||
| + | \end{align}</math>}} | ||
| - | <center> [[ | + | and the whole equation then has standard form, |
| - | + | ||
| + | {{Displayed math||<math>\begin{align} | ||
| + | (x-1)^2 - 1 + (y+3)^2 - 9 &= -3\,,\\[5pt] | ||
| + | (x-1)^2 + (y+3)^2 &= 7\,\textrm{.} | ||
| + | \end{align}</math>}} | ||
| + | |||
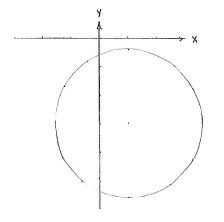
| + | From this, we see that the circle has its centre at (1,-3) and radius <math>\sqrt{7}\,</math>. | ||
| + | |||
| + | |||
| + | <center> [[Image:4_1_7_c.gif]] </center> | ||
Current revision
By completing the square, we can rewrite the x- and y-terms as quadratic expressions,
| \displaystyle \begin{align}
x^2 - 2x &= (x-1)^2 - 1^2\,,\\[5pt] y^2 + 6y &= (y+3)^2 - 3^2\,, \end{align} |
and the whole equation then has standard form,
| \displaystyle \begin{align}
(x-1)^2 - 1 + (y+3)^2 - 9 &= -3\,,\\[5pt] (x-1)^2 + (y+3)^2 &= 7\,\textrm{.} \end{align} |
From this, we see that the circle has its centre at (1,-3) and radius \displaystyle \sqrt{7}\,.