Solution 4.1:6a
From Förberedande kurs i matematik 1
(Difference between revisions)
m |
|||
| (3 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
| - | + | If we write the equation as | |
| - | + | ||
| - | <center> [[ | + | {{Displayed math||<math>(x-0)^2 + (y-0)^2 = 9</math>}} |
| - | + | ||
| + | we can interpret the left-hand side as the square of the distance between the points (''x'',''y'') and (0,0). The whole equation says that the distance from a point (''x'',''y'') to the origin should be constant and equal to <math>\sqrt{9}=3\,</math>, which describes a circle with its centre at the origin and radius 3. | ||
| + | |||
| + | |||
| + | <center> [[Image:4_1_6_a.gif]] </center> | ||
Current revision
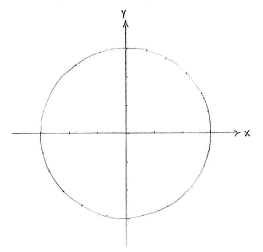
If we write the equation as
| \displaystyle (x-0)^2 + (y-0)^2 = 9 |
we can interpret the left-hand side as the square of the distance between the points (x,y) and (0,0). The whole equation says that the distance from a point (x,y) to the origin should be constant and equal to \displaystyle \sqrt{9}=3\,, which describes a circle with its centre at the origin and radius 3.