2. Algebra
From Förberedande kurs i matematik 1
(Ny sida: __NOTOC__ <!-- Don't remove this line --> <!-- A hack to get a popup-window --> {|align="left" | width="220" height="203" |<math>\text{@(a class="image" href="http://smaug.nti.se/temp/KT...) |
|||
| (9 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| - | <!-- Don't remove this line --> | ||
| + | Algebra is the branch of mathematics that is concerned with symbolic expressions and variables, not just calculations with numbers. | ||
| + | Algebra is needed in many situations. For example, it can be used to represent situations in which one or more of the quantities is unknown, and hence perhaps to find the values of these quantities. It can also be used to represent geometrical structures, such as curves on the plane. | ||
| - | + | In some cases, too, we use symbols because it is important that a number be exactly specified; perhaps, for example, a circle is to have a circumference of exactly <math>4\pi</math> units, or the hypotenuse of a triangle is to be <math>\sqrt{3}</math>, or the value of a constant is to be exactly <math>\dfrac{1-\ln 2}{3}</math>. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | '''Varför räknar vi med bokstäver och vem kom på detta?''' | ||
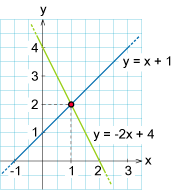
| + | [[Image:grafisk lösning.gif|thumb|250px|A linear equation with two unknowns can be interpreted as a straight line in a coordinate system. The solution (''x'',''y'') of these two simultaneous equations corresponds to the common point of these lines, that is their point of intersection. ]] | ||
| + | Then it may be easier just to call the number, for example, ''a''. In return you must accept that at the end of a calculation, you may not arrive at a numerical value, but instead may finish up with an expression that contains ''a''. | ||
| - | + | A common situation where algebra may be necessary is simplification. It is often very important to simplify an expression, such as before differentiation, or when an equation is to be solved. | |
| + | Simplification reduces the risk of careless mistakes and avoids unnecessary work. To simplify means to transform an expression from one form to another, which exactly equivalent mathematically but which is in some sense simpler. What is meant by ”simple” is sometimes obvious, but it can also depend on what you want to do with the expression. | ||
| + | When differentiating, it may be advantageous to transform the expression into a sum of a number of terms. On the other hand when we solve an equation, it may be advantageous to reformulate the expression as a product of a number of factors. Therefore, one needs to be proficient in converting expressions into different forms. | ||
| + | '''It is important to note that the material in this section— as well as in other parts of the course — is designed so that one does not use calculators.''' | ||
| + | ''Calculators are not used at all on some degree courses, and on others their use is limited.'' | ||
| + | <div class="inforuta" style="width:580px;"> | ||
| + | '''To do well in Algebra''' | ||
| + | # Start by reading the section's theory and study the examples. | ||
| + | #Work through the exercises and try to solve them without using a calculator. Make sure that you have the right answer by clicking on the answer button. If you do not have it, you can click on the solution button to see what went wrong | ||
| + | #Then go ahead and answer the questions in the basic test of the section. | ||
| + | # If you get stuck on a point, check to see if someone else has discussed the point in the forum belonging to the section. If not, take up the point yourself. Your teacher (or a student) will respond to your question within a few hours. | ||
| + | #When you have finished with the exercises and the basic test in a section you should take the final test to get a pass for the section. The requirement here is to answer correctly three questions in a row before you can move on to the next section. | ||
| + | # When you have answered all the questions correctly in both the basic and the final test of this section you will have a pass for this section and can move on to Part 3 of the course. | ||
| - | + | P.S. If you feel that you are very familiar with the contents of a section you can test yourself by going directly to the basic and final tests. You must answer all the questions correctly in a test, but you may do the test several times if you do not succeed at the first attempt. It is your final results that will appear in the statistics. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | | + | |
</div> | </div> | ||
Current revision
Algebra is the branch of mathematics that is concerned with symbolic expressions and variables, not just calculations with numbers.
Algebra is needed in many situations. For example, it can be used to represent situations in which one or more of the quantities is unknown, and hence perhaps to find the values of these quantities. It can also be used to represent geometrical structures, such as curves on the plane.
In some cases, too, we use symbols because it is important that a number be exactly specified; perhaps, for example, a circle is to have a circumference of exactly \displaystyle 4\pi units, or the hypotenuse of a triangle is to be \displaystyle \sqrt{3}, or the value of a constant is to be exactly \displaystyle \dfrac{1-\ln 2}{3}.
Then it may be easier just to call the number, for example, a. In return you must accept that at the end of a calculation, you may not arrive at a numerical value, but instead may finish up with an expression that contains a.
A common situation where algebra may be necessary is simplification. It is often very important to simplify an expression, such as before differentiation, or when an equation is to be solved.
Simplification reduces the risk of careless mistakes and avoids unnecessary work. To simplify means to transform an expression from one form to another, which exactly equivalent mathematically but which is in some sense simpler. What is meant by ”simple” is sometimes obvious, but it can also depend on what you want to do with the expression.
When differentiating, it may be advantageous to transform the expression into a sum of a number of terms. On the other hand when we solve an equation, it may be advantageous to reformulate the expression as a product of a number of factors. Therefore, one needs to be proficient in converting expressions into different forms.
It is important to note that the material in this section— as well as in other parts of the course — is designed so that one does not use calculators.
Calculators are not used at all on some degree courses, and on others their use is limited.
To do well in Algebra
- Start by reading the section's theory and study the examples.
- Work through the exercises and try to solve them without using a calculator. Make sure that you have the right answer by clicking on the answer button. If you do not have it, you can click on the solution button to see what went wrong
- Then go ahead and answer the questions in the basic test of the section.
- If you get stuck on a point, check to see if someone else has discussed the point in the forum belonging to the section. If not, take up the point yourself. Your teacher (or a student) will respond to your question within a few hours.
- When you have finished with the exercises and the basic test in a section you should take the final test to get a pass for the section. The requirement here is to answer correctly three questions in a row before you can move on to the next section.
- When you have answered all the questions correctly in both the basic and the final test of this section you will have a pass for this section and can move on to Part 3 of the course.
P.S. If you feel that you are very familiar with the contents of a section you can test yourself by going directly to the basic and final tests. You must answer all the questions correctly in a test, but you may do the test several times if you do not succeed at the first attempt. It is your final results that will appear in the statistics.