Solution 4.4:1d

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (13:16, 10 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
Because
+
Because <math>\tan v = \frac{\sin v}{\cos v}</math>, the condition <math>\tan v = 1</math> gives <math>\sin v = \cos v</math>, i.e. we look for angles in the unit circle whose ''x''- and ''y''-coordinates are equal.
-
<math>\tan v=\frac{\sin v}{\cos v}</math>, the condition
+
-
<math>\text{tan }v=\text{1 }</math>
+
-
gives
+
-
<math>\text{sin }v=\text{ cos }v</math>, i.e. we look for angles in the unit circle whose
+
-
<math>x</math>
+
-
- and
+
-
<math>y</math>
+
-
-coordinates are equal.
+
-
 
+
-
After drawing the unit circle and the line y=x, we see that there are two angles which satisfy these conditions,
+
-
<math>v={\pi }/{4}\;</math>
+
-
and
+
-
<math>v=\pi +{\pi }/{4}\;={5\pi }/{4}\;</math>
+
-
 
+
-
 
+
 +
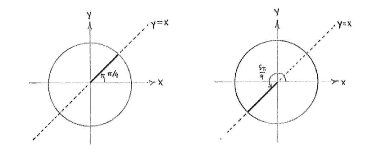
After drawing the unit circle and the line y=x, we see that there are two angles which satisfy these conditions, <math>v=\pi/4</math> and <math>v = \pi + \pi/4 = 5\pi/4\,</math>.
[[Image:4_4_1_d.gif|center]]
[[Image:4_4_1_d.gif|center]]

Current revision

Because \displaystyle \tan v = \frac{\sin v}{\cos v}, the condition \displaystyle \tan v = 1 gives \displaystyle \sin v = \cos v, i.e. we look for angles in the unit circle whose x- and y-coordinates are equal.

After drawing the unit circle and the line y=x, we see that there are two angles which satisfy these conditions, \displaystyle v=\pi/4 and \displaystyle v = \pi + \pi/4 = 5\pi/4\,.

Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_4.4:1d"