Solution 4.3:3e

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Robot: Automated text replacement (-[[Bild: +[[Image:))
Current revision (12:22, 10 October 2008) (edit) (undo)
m
 
(3 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
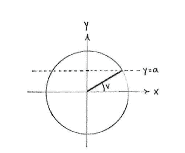
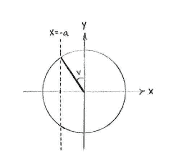
The angle <math>\pi/2+v</math> makes the same angle with the positive ''y''-axis as the angle ''v'' makes with the positive ''x''-axis, and hence we see that the ''x''-coordinate for <math>\pi/2+v</math> is equal to the ''y''-coordinate for ''v'', but with a change of sign, i.e.
-
<center> [[Image:4_3_3e.gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
-
[[Image:4_3_3_e.gif|center]]
+
{{Displayed math||<math>\cos \Bigl(\frac{\pi}{2}+v\Bigr) = -\sin v = -a\,\textrm{.}</math>}}
 +
 
 +
{| align="center"
 +
|align="center"|[[Image:4_3_3_e-1.gif|center]]
 +
|align="center"|[[Image:4_3_3_e-2.gif|center]]
 +
|-
 +
|align="center"|<small>Angle ''v''</small>
 +
|align="center"|<small>Angle π/2&nbsp;+&nbsp;''v''</small>
 +
|}

Current revision

The angle \displaystyle \pi/2+v makes the same angle with the positive y-axis as the angle v makes with the positive x-axis, and hence we see that the x-coordinate for \displaystyle \pi/2+v is equal to the y-coordinate for v, but with a change of sign, i.e.

\displaystyle \cos \Bigl(\frac{\pi}{2}+v\Bigr) = -\sin v = -a\,\textrm{.}
Angle v Angle π/2 + v
Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_4.3:3e"