Solution 4.2:1f
From Förberedande kurs i matematik 1
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
| + | The side adjacent to the angle of 50° is marked ''x'' and the opposite is the side of length 19. | ||
| + | |||
[[Image:4_2_1_f.gif|center]] | [[Image:4_2_1_f.gif|center]] | ||
| - | + | If we write the tangent for the angle, this gives a relation which contains ''x'' as the only unknown, | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | If we write the tangent for the angle, this gives a relation which contains | + | |
| - | + | ||
| - | as the only unknown, | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\tan 50^{\circ} = \frac{19}{x}\,\textrm{.}</math>}} | ||
This gives | This gives | ||
| - | + | {{Displayed math||<math>x=\frac{19}{\tan 50^{\circ }}\quad ({}\approx 15\textrm{.}9)\,\textrm{.}</math>}} | |
| - | <math>x=\frac{19}{\tan 50^{\circ }}\quad | + | |
Current revision
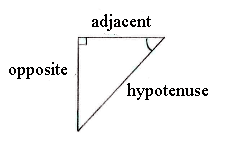
The side adjacent to the angle of 50° is marked x and the opposite is the side of length 19.
If we write the tangent for the angle, this gives a relation which contains x as the only unknown,
| \displaystyle \tan 50^{\circ} = \frac{19}{x}\,\textrm{.} |
This gives
| \displaystyle x=\frac{19}{\tan 50^{\circ }}\quad ({}\approx 15\textrm{.}9)\,\textrm{.} |