Solution 4.2:1d
From Förberedande kurs i matematik 1
(Difference between revisions)
m (Lösning 4.2:1d moved to Solution 4.2:1d: Robot: moved page) |
m |
||
| (One intermediate revision not shown.) | |||
| Line 1: | Line 1: | ||
| - | + | The side marked ''x'' is the hypotenuse in the right-angled triangle and the side of length 16 is the adjacent to the angle of 20°. | |
| - | + | ||
| - | + | ||
[[Image:4_2_1_d.gif|center]] | [[Image:4_2_1_d.gif|center]] | ||
| + | |||
| + | By writing the quotient for <math>\cos 20^{\circ}</math>, we obtain the relation | ||
| + | |||
| + | {{Displayed math||<math>\cos 20^{\circ} = \frac{16}{x}</math>}} | ||
| + | |||
| + | and this gives | ||
| + | |||
| + | {{Displayed math||<math>x = \frac{16}{\cos20^{\circ}}\quad ({}\approx 17\textrm{.}0)\,\textrm{.}</math>}} | ||
Current revision
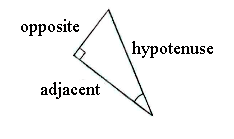
The side marked x is the hypotenuse in the right-angled triangle and the side of length 16 is the adjacent to the angle of 20°.
By writing the quotient for \displaystyle \cos 20^{\circ}, we obtain the relation
| \displaystyle \cos 20^{\circ} = \frac{16}{x} |
and this gives
| \displaystyle x = \frac{16}{\cos20^{\circ}}\quad ({}\approx 17\textrm{.}0)\,\textrm{.} |