From Förberedande kurs i matematik 1

Revision as of 07:06, 21 August 2008 (edit) Tekbot (Talk | contribs) m (Robot: Automated text replacement (-[[Bild: +[[Image:)) ← Previous diff		Current revision (11:23, 8 October 2008) (edit) (undo) Tek (Talk | contribs) m
(2 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	The equation is almost in the standard form for a circle; all that is needed is for us to collect together the ''y''²- and ''y''-terms into a quadratic term by completing the square
-	<center> [[Image:4_1_7_b.gif]] </center>	+
-	<center> [[Image:4_1_7b.gif]] </center>	+	{{Displayed math||<math>y^2 + 4y = (y+2)^2 - 2^2\,\textrm{.}</math>}}
-	{{NAVCONTENT_STOP}}	+
		+	After rewriting, the equation is
		+
		+	{{Displayed math||<math>x^2 + (y+2)^2 = 4</math>}}
		+
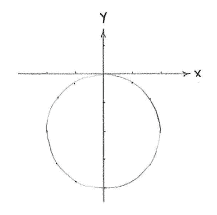
		+	and we see that the equation describes a circle having its centre at (0,-2) and radius <math>\sqrt{4}=2\,</math>.
		+
		+
		+	<center> [[Image:4_1_7_b.gif]] </center>

---

Current revision

The equation is almost in the standard form for a circle; all that is needed is for us to collect together the y²- and y-terms into a quadratic term by completing the square

\displaystyle y^2 + 4y = (y+2)^2 - 2^2\,\textrm{.}

After rewriting, the equation is

\displaystyle x^2 + (y+2)^2 = 4

and we see that the equation describes a circle having its centre at (0,-2) and radius \displaystyle \sqrt{4}=2\,.