From Förberedande kurs i matematik 1

Revision as of 14:14, 15 August 2008 (edit) Martin (Talk | contribs) ← Previous diff		Current revision (08:31, 8 October 2008) (edit) (undo) Tek (Talk | contribs) m
(3 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	If we write the equation as
-	<center> [[Bild:4_1_6_a.gif]] </center>	+
-	<center> [[Bild:4_1_6a.gif]] </center>	+	{{Displayed math||<math>(x-0)^2 + (y-0)^2 = 9</math>}}
-	{{NAVCONTENT_STOP}}	+
		+	we can interpret the left-hand side as the square of the distance between the points (''x'',''y'') and (0,0). The whole equation says that the distance from a point (''x'',''y'') to the origin should be constant and equal to <math>\sqrt{9}=3\,</math>, which describes a circle with its centre at the origin and radius 3.
		+
		+
		+	<center> [[Image:4_1_6_a.gif]] </center>

---

Current revision

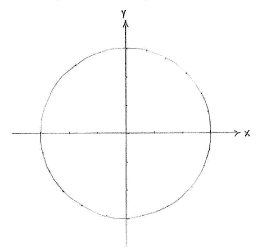
If we write the equation as

\displaystyle (x-0)^2 + (y-0)^2 = 9

we can interpret the left-hand side as the square of the distance between the points (x,y) and (0,0). The whole equation says that the distance from a point (x,y) to the origin should be constant and equal to \displaystyle \sqrt{9}=3\,, which describes a circle with its centre at the origin and radius 3.