Solution 4.1:5a
From Förberedande kurs i matematik 1
(Difference between revisions)
m (Lösning 4.1:5a moved to Solution 4.1:5a: Robot: moved page) |
m |
||
| (One intermediate revision not shown.) | |||
| Line 1: | Line 1: | ||
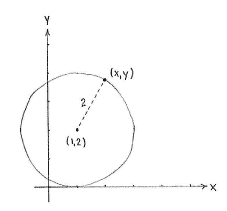
| - | + | A circle is defined as all the points which have a fixed distance to the circle's midpoint. Hence, a point (''x'',''y'') lies on our circle if and only if its distance to the point (1,3) is exactly 2. Using the distance formula, we can express this condition as | |
| - | + | ||
| - | < | + | {{Displayed math||<math>\sqrt{(x-1)^2 + (y-2)^2} = 2\,\textrm{.}</math>}} |
| - | {{ | + | |
| + | After squaring, we obtain the equation of the circle in standard form, | ||
| + | |||
| + | {{Displayed math||<math>(x-1)^2 + (y-2)^2 = 4\,\textrm{.}</math>}} | ||
| + | |||
| + | |||
| + | [[Image:4_1_5_a.gif|center]] | ||
Current revision
A circle is defined as all the points which have a fixed distance to the circle's midpoint. Hence, a point (x,y) lies on our circle if and only if its distance to the point (1,3) is exactly 2. Using the distance formula, we can express this condition as
| \displaystyle \sqrt{(x-1)^2 + (y-2)^2} = 2\,\textrm{.} |
After squaring, we obtain the equation of the circle in standard form,
| \displaystyle (x-1)^2 + (y-2)^2 = 4\,\textrm{.} |