Solution 4.4:1a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 4.4:1a moved to Solution 4.4:1a: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
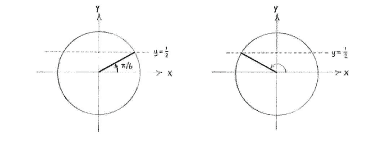
In the unit circle's first quadrant, there is one angle whose sine value equals
-
<center> [[Image:4_4_1a.gif]] </center>
+
<math>\frac{1}{2}</math>
-
{{NAVCONTENT_STOP}}
+
and that is
 +
<math>v={\pi }/{6}\;</math>.
[[Image:4_4_1_a.gif|center]]
[[Image:4_4_1_a.gif|center]]
 +
 +
From the figures, we see that there is a further angle with the same sine value and it lies in the second quadrant. Because of symmetry, it makes the same angle with the negative
 +
<math>x</math>
 +
-axis as
 +
<math>v={\pi }/{6}\;</math>
 +
makes with the positive
 +
<math>x</math>
 +
-axis, i.e. the other angle is
 +
<math>v=\pi -{\pi }/{6}\;={5\pi }/{6}\;</math>

Revision as of 11:58, 30 September 2008

In the unit circle's first quadrant, there is one angle whose sine value equals \displaystyle \frac{1}{2} and that is \displaystyle v={\pi }/{6}\;.

From the figures, we see that there is a further angle with the same sine value and it lies in the second quadrant. Because of symmetry, it makes the same angle with the negative \displaystyle x -axis as \displaystyle v={\pi }/{6}\; makes with the positive \displaystyle x -axis, i.e. the other angle is \displaystyle v=\pi -{\pi }/{6}\;={5\pi }/{6}\;

Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_4.4:1a"