Solution 4.3:6a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 4.3:6a moved to Solution 4.3:6a: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
If we think of the angle v as an angle in the unit circle, then
-
<center> [[Image:4_3_6a-1(2).gif]] </center>
+
<math>v</math>
-
{{NAVCONTENT_STOP}}
+
lies in the fourth quadrant and has
-
{{NAVCONTENT_START}}
+
<math>x</math>
-
<center> [[Image:4_3_6a-2(2).gif]] </center>
+
-coordinate
-
{{NAVCONTENT_STOP}}
+
<math>\frac{3}{4}</math>.
 +
 
[[Image:4_3_6_a1.gif|center]]
[[Image:4_3_6_a1.gif|center]]
 +
 +
If we enlarge the fourth quadrant, we see that we can make a right-angled triangle with hypotenuse equal to
 +
<math>\text{1}</math>
 +
and an opposite side equal to
 +
<math>\frac{3}{4}</math>.
 +
[[Image:4_3_6_a2.gif|center]]
[[Image:4_3_6_a2.gif|center]]
 +
 +
Using Pythagoras' theorem, it is possible to determine the remaining side from
 +
 +
 +
 +
<math>b^{2}+\left( \frac{3}{4} \right)^{2}=1^{2}</math>
 +
 +
 +
which gives that
 +
 +
 +
<math>\begin{align}
 +
& b^{2}+\left( \frac{3}{4} \right)^{2}=1^{2} \\
 +
& b=\sqrt{1-\left( \frac{3}{4} \right)^{2}}=\sqrt{1-\frac{9}{16}}=\sqrt{\frac{7}{16}}=\frac{\sqrt{7}}{4} \\
 +
\end{align}</math>
 +
 +
 +
Because the angle
 +
<math>v</math>
 +
belongs to the fourth quadrant, its
 +
<math>y</math>
 +
-coordinate is negative and is therefore equal to
 +
<math>-b</math>, i.e.
 +
 +
 +
<math>\sin v=-\frac{\sqrt{7}}{4}</math>
 +
 +
 +
Thus, we have directly that
 +
 +
 +
<math>\tan v=\frac{\sin v}{\cos v}=\frac{-\frac{\sqrt{7}}{4}}{\frac{3}{4}}=-\frac{\sqrt{7}}{3}</math>

Revision as of 09:12, 30 September 2008

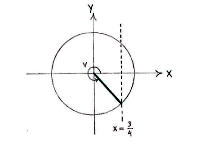
If we think of the angle v as an angle in the unit circle, then \displaystyle v lies in the fourth quadrant and has \displaystyle x -coordinate \displaystyle \frac{3}{4}.


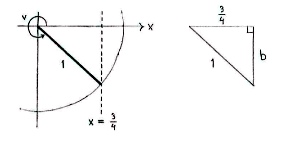
If we enlarge the fourth quadrant, we see that we can make a right-angled triangle with hypotenuse equal to \displaystyle \text{1} and an opposite side equal to \displaystyle \frac{3}{4}.

Using Pythagoras' theorem, it is possible to determine the remaining side from


\displaystyle b^{2}+\left( \frac{3}{4} \right)^{2}=1^{2}


which gives that


\displaystyle \begin{align} & b^{2}+\left( \frac{3}{4} \right)^{2}=1^{2} \\ & b=\sqrt{1-\left( \frac{3}{4} \right)^{2}}=\sqrt{1-\frac{9}{16}}=\sqrt{\frac{7}{16}}=\frac{\sqrt{7}}{4} \\ \end{align}


Because the angle \displaystyle v belongs to the fourth quadrant, its \displaystyle y -coordinate is negative and is therefore equal to \displaystyle -b, i.e.


\displaystyle \sin v=-\frac{\sqrt{7}}{4}


Thus, we have directly that


\displaystyle \tan v=\frac{\sin v}{\cos v}=\frac{-\frac{\sqrt{7}}{4}}{\frac{3}{4}}=-\frac{\sqrt{7}}{3}

Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_4.3:6a"