Solution 4.3:3b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 4.3:3b moved to Solution 4.3:3b: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The angle
-
<center> [[Image:4_3_3b.gif]] </center>
+
<math>\pi -v\text{ }</math>
-
{{NAVCONTENT_STOP}}
+
makes the same angle with the negative
 +
<math>x</math>
 +
-axis as the angle
 +
<math>v</math>
 +
makes with the positive
 +
<math>x</math>
 +
-axis and this means that
 +
<math>\pi -v\text{ }</math>
 +
is the reflection of
 +
<math>v</math>
 +
in the y-axis.
 +
 
[[Image:4_3_3_b.gif|center]]
[[Image:4_3_3_b.gif|center]]
 +
 +
Under such reflection, the angle's
 +
<math>y</math>
 +
-coordinate does not change (but the
 +
<math>x</math>
 +
-coordinate changes sign) and therefore
 +
<math>\text{sin}\left( \pi -v \right)=\text{sin }v\text{ }=a</math>.

Revision as of 10:51, 29 September 2008

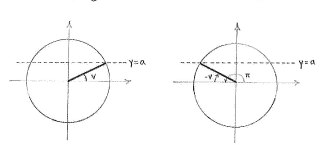
The angle \displaystyle \pi -v\text{ } makes the same angle with the negative \displaystyle x -axis as the angle \displaystyle v makes with the positive \displaystyle x -axis and this means that \displaystyle \pi -v\text{ } is the reflection of \displaystyle v in the y-axis.

Under such reflection, the angle's \displaystyle y -coordinate does not change (but the \displaystyle x -coordinate changes sign) and therefore \displaystyle \text{sin}\left( \pi -v \right)=\text{sin }v\text{ }=a.

Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_4.3:3b"