Solution 2.3:9a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 2.3:9a moved to Solution 2.3:9a: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
A point lies on the
-
<center> [[Image:2_3_9a.gif]] </center>
+
<math>x</math>
-
{{NAVCONTENT_STOP}}
+
-axis if it has
 +
<math>y</math>
 +
-coordinate
 +
<math>0</math>
 +
and we therefore look for all the points on the curve
 +
<math>y=x^{\text{2}}-\text{1}</math>
 +
where
 +
<math>y=0</math>, i.e. all points which satisfy the equation
 +
 
 +
 
 +
<math>0=x^{\text{2}}-\text{1}</math>
 +
 
 +
 
 +
This equation has solutions
 +
<math>x=\pm \text{1}</math>, which means that the points of intersection are
 +
<math>\left( -1 \right.,\left. 0 \right)</math>
 +
and
 +
<math>\left( 1 \right.,\left. 0 \right)</math>.
 +
 
 +
 
[[Image:2_3_9_a.gif|center]]
[[Image:2_3_9_a.gif|center]]

Revision as of 11:43, 21 September 2008

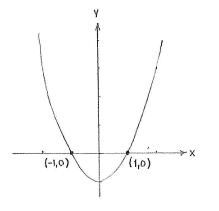
A point lies on the \displaystyle x -axis if it has \displaystyle y -coordinate \displaystyle 0 and we therefore look for all the points on the curve \displaystyle y=x^{\text{2}}-\text{1} where \displaystyle y=0, i.e. all points which satisfy the equation


\displaystyle 0=x^{\text{2}}-\text{1}


This equation has solutions \displaystyle x=\pm \text{1}, which means that the points of intersection are \displaystyle \left( -1 \right.,\left. 0 \right) and \displaystyle \left( 1 \right.,\left. 0 \right).


Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_2.3:9a"