From Förberedande kurs i matematik 2

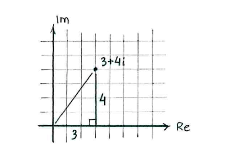
The magnitude of the number \displaystyle 3+4i is the number's distance to the origin in the complex number plane.

If we treat the line from the origin to \displaystyle 3+4i as the hypotenuse in a right-angled triangle which has its legs parallel with the real and imaginary axes, then the Pythagorean theorem gives that the magnitude is

\displaystyle |3+4i| = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5\,\textrm{.}

Note: In general, the magnitude of a complex number \displaystyle z=x+iy is equal to

\displaystyle |z| = |x+iy| = \sqrt{x^2+y^2}\,\textrm{.}