From Förberedande kurs i matematik 2

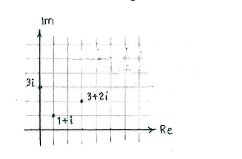
If we mark the three complex numbers in the plane, we see that the fourth corner will have \displaystyle 3+2i and \displaystyle 3i as neighbouring corners.

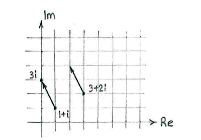
In order to find the fourth corner, we use the fact that in a square opposite sides are parallel and all sides have the same length. This means that the vector from \displaystyle 1+i to \displaystyle 3i is equal to the vector from \displaystyle 3+2i to the fourth corner.

If we interpret the complex numbers as vectors, this means that the vector from \displaystyle 1+i to \displaystyle \text{3}i is

\displaystyle 3i-(1+i) = -1+2i

and we obtain the fourth corner if we add this vector to the corner \displaystyle 3+2i,

\displaystyle 3+2i+(-1+2i) = 2+4i\,\textrm{.}