From Förberedande kurs i matematik 2

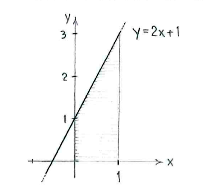
The graph of the function \displaystyle y=2x+1 is a straight line which cuts the \displaystyle y -axis at \displaystyle y=\text{1} and has gradient \displaystyle 2.

The integral's value is the area under the straight line and between \displaystyle x=0\text{ } and \displaystyle x=\text{1}.

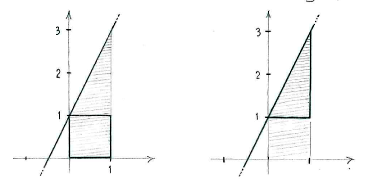
We can divide up the region under the graph into a square and rectangle,

and then add up the area to obtain the total area.

The value of the integral is

\displaystyle \int\limits_{0}^{1}{\left( 2x+1 \right)\,}dx= (area of the square) + (area of the triangle) \displaystyle 1\centerdot 1+\frac{1}{2}\centerdot 1\centerdot 2=2