From Förberedande kurs i matematik 2

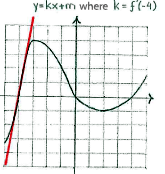
The derivative \displaystyle {f}'\left( -4 \right) gives the function's instantaneous rate of change at the point \displaystyle x=-\text{4}, i.e. it is a measure of the function's value changes in the vicinity of \displaystyle x=-\text{4}.

In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point \displaystyle x=-\text{4}.

\displaystyle y=kx+m\text{ } where \displaystyle k={f}'\left( -\text{4} \right)

Because the tangent is sloping upwards, it has a positive gradient and therefore \displaystyle {f}'\left( -\text{4} \right)>0.

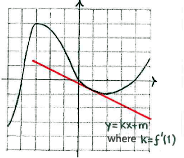
At the point \displaystyle x=\text{1}, the tangent slopes downwards and this means that \displaystyle {f}'\left( \text{1} \right)<0.

\displaystyle y=kx+m\text{ } where \displaystyle k={f}'\left( 1 \right)