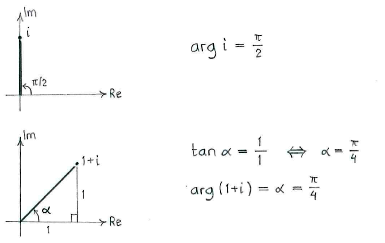From Förberedande kurs i matematik 2

When dividing two complex numbers, the numerator's magnitude is divided by the denominator's absolute value and the numerator's argument is subtracted from the numerator's argument.

The argument of the quotient \displaystyle \frac{i}{1+i} is therefore

\displaystyle \arg \frac{i}{1+i}=\arg i-\arg \left( 1+i \right)

We obtain the argument of \displaystyle i and \displaystyle \text{1}+i by drawing the numbers in the complex plane and using a little trigonometry:

Hence, we obtain

\displaystyle \arg \frac{i}{1+i}=\arg i-\arg \left( 1+i \right)=\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}