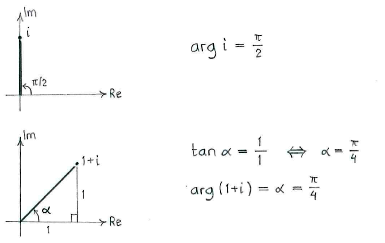From Förberedande kurs i matematik 2

When dividing two complex numbers, the numerator's magnitude is divided by the denominator's magnitude and the numerator's argument is subtracted from the numerator's argument.

The argument of the quotient \displaystyle i/(1+i) is therefore

\displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.}

We obtain the argument of \displaystyle i and \displaystyle 1+i by drawing the numbers in the complex plane and using a little trigonometry.

Hence, we obtain

\displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.}