From Förberedande kurs i matematik 2

Revision as of 12:10, 7 April 2008 (edit) Oskar (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:3_2_4a.gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (09:54, 29 October 2008) (edit) (undo) Tek (Talk | contribs) m
(4 intermediate revisions not shown.)
Line 1:		Line 1:
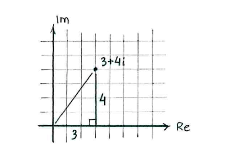
-	{{NAVCONTENT_START}}	+	The magnitude of the number <math>3+4i</math> is the number's distance to the origin in the complex number plane.
-	<center> [[Bild:3_2_4a.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	If we treat the line from the origin to <math>3+4i</math> as the hypotenuse in a right-angled triangle which has its legs parallel with the real and imaginary axes, then the Pythagorean theorem gives that the magnitude is
		+
		+	{{Displayed math||<math>|3+4i| = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5\,\textrm{.}</math>}}
		+
		+	[[Image:3_2_4_a.gif|center]]
		+
		+
		+	Note: In general, the magnitude of a complex number <math>z=x+iy</math> is equal to
		+
		+	{{Displayed math||<math>|z| = |x+iy| = \sqrt{x^2+y^2}\,\textrm{.}</math>}}

---

Current revision

The magnitude of the number \displaystyle 3+4i is the number's distance to the origin in the complex number plane.

If we treat the line from the origin to \displaystyle 3+4i as the hypotenuse in a right-angled triangle which has its legs parallel with the real and imaginary axes, then the Pythagorean theorem gives that the magnitude is

\displaystyle |3+4i| = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5\,\textrm{.}

Note: In general, the magnitude of a complex number \displaystyle z=x+iy is equal to

\displaystyle |z| = |x+iy| = \sqrt{x^2+y^2}\,\textrm{.}