From Förberedande kurs i matematik 2

Revision as of 12:07, 7 April 2008 (edit) Oskar (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:3_2_2e.gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (09:44, 29 October 2008) (edit) (undo) Tek (Talk | contribs) m
(4 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	Because the expression contains both <math>z</math> and <math>\bar{z}</math>, we write out <math>z=x+iy</math>, where <math>x</math> is the real part of <math>z</math> and <math>y</math> is the imaginary part. Thus, we have
-	<center> [[Bild:3_2_2e.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	:*<math>\mathop{\rm Re}z = x</math>
		+	:*<math>i+\bar{z} = i+(x-iy) = x+(1-y)i</math>
		+
		+	and the condition becomes
		+
		+	{{Displayed math||<math>x=x+(1-y)i\quad\Leftrightarrow\quad 0=(1-y)i</math>}}
		+
		+	which means that <math>y=1</math>.
		+
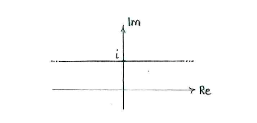
		+	The set therefore consists of all complex numbers with imaginary part 1.
		+
		+	[[Image:3_2_2_e.gif|center]]

---

Current revision

Because the expression contains both \displaystyle z and \displaystyle \bar{z}, we write out \displaystyle z=x+iy, where \displaystyle x is the real part of \displaystyle z and \displaystyle y is the imaginary part. Thus, we have

• \displaystyle \mathop{\rm Re}z = x
• \displaystyle i+\bar{z} = i+(x-iy) = x+(1-y)i

and the condition becomes

\displaystyle x=x+(1-y)i\quad\Leftrightarrow\quad 0=(1-y)i

which means that \displaystyle y=1.

The set therefore consists of all complex numbers with imaginary part 1.