From Förberedande kurs i matematik 2

Revision as of 09:23, 7 April 2008 (edit) Oskar (Talk | contribs) ← Previous diff		Current revision (12:57, 28 October 2008) (edit) (undo) Tek (Talk | contribs) m
(4 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	The integral is a standard integral, with <math>5x</math> as the argument of the cosine function. If we therefore substitute <math>u=5x</math>, we obtain the “correct” argument of the cosine,
-	<center> [[Bild:2_2_2a-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{{Displayed math||<math>\int\limits_0^{\pi} \cos 5x\,dx = \left\{\begin{align}
-	{{NAVCONTENT_START}}	+	u &= 5x\\[5pt]
-	<center> [[Bild:2_2_2a-2(2).gif]] </center>	+	du &= (5x)'\,dx = 5\,dx
-	{{NAVCONTENT_STOP}}	+	\end{align}\right\} = \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du\,\textrm{.}</math>}}
		+
		+	As can be seen, the variable change replaced <math>dx</math> by <math>\tfrac{1}{5}\,du</math> and the new limits of integration become <math>u=5\cdot 0=0</math>
		+	and <math>u=5\cdot \pi = 5\pi\,</math>.
		+
		+	Now, we have a standard integral which we can easily compute,
		+
		+	{{Displayed math||<math>\frac{1}{5}\int\limits_0^{5\pi} \cos u\,du = \frac{1}{5}\Bigl[\ \sin u\ \Bigr]_0^{5\pi} = \frac{1}{5}( \sin 5\pi -\sin 0) = \frac{1}{5}(0-0) = 0\,\textrm{.}</math>}}
		+
		+
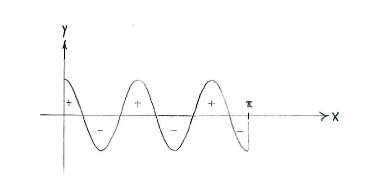
		+	Note: If we draw the graph of <math>y=\cos 5x</math>, we see also that the area between the curve and ''x''-axis above the ''x''-axis is the same as the area under the ''x''-axis.
		+
		+	[[Image:2_2_2_a.gif|center]]

---

Current revision

The integral is a standard integral, with \displaystyle 5x as the argument of the cosine function. If we therefore substitute \displaystyle u=5x, we obtain the “correct” argument of the cosine,

\displaystyle \int\limits_0^{\pi} \cos 5x\,dx = \left\{\begin{align} u &= 5x\\[5pt] du &= (5x)'\,dx = 5\,dx \end{align}\right\} = \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du\,\textrm{.}

As can be seen, the variable change replaced \displaystyle dx by \displaystyle \tfrac{1}{5}\,du and the new limits of integration become \displaystyle u=5\cdot 0=0 and \displaystyle u=5\cdot \pi = 5\pi\,.

Now, we have a standard integral which we can easily compute,

\displaystyle \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du = \frac{1}{5}\Bigl[\ \sin u\ \Bigr]_0^{5\pi} = \frac{1}{5}( \sin 5\pi -\sin 0) = \frac{1}{5}(0-0) = 0\,\textrm{.}

Note: If we draw the graph of \displaystyle y=\cos 5x, we see also that the area between the curve and x-axis above the x-axis is the same as the area under the x-axis.