From Förberedande kurs i matematik 2

Revision as of 08:01, 7 April 2008 (edit) Oskar (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:2_1_1a.gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (12:04, 21 October 2008) (edit) (undo) Tek (Talk | contribs) m
(4 intermediate revisions not shown.)
Line 1:		Line 1:
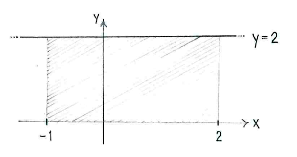
-	{{NAVCONTENT_START}}	+	The value of the integral can be interpreted as the area under the graph <math>y=2</math> from <math>x=-1\ </math> to <math>x=2</math>.
-	<center> [[Bild:2_1_1a.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	[[Image:2_1_1_a.gif|center]]
		+
		+	Because the region is a rectangle, we can determine its area directly and obtain
		+
		+	{{Displayed math||<math>\int\limits_{-1}^{2} 2\,dx = \text{(base)}\cdot\text{(height)} = 3\cdot 2 = 6\,\textrm{.}</math>}}

---

Current revision

The value of the integral can be interpreted as the area under the graph \displaystyle y=2 from \displaystyle x=-1\ to \displaystyle x=2.

Because the region is a rectangle, we can determine its area directly and obtain

\displaystyle \int\limits_{-1}^{2} 2\,dx = \text{(base)}\cdot\text{(height)} = 3\cdot 2 = 6\,\textrm{.}