Solution 3.2:1c

From Förberedande kurs i matematik 2

(Difference between revisions)
Jump to: navigation, search
m (Robot: Automated text replacement (-[[Bild: +[[Image:))
Current revision (09:23, 29 October 2008) (edit) (undo)
m
 
(2 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
By calculation, we obtain
-
<center> [[Image:3_2_1c.gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
 +
{{Displayed math||<math>2z+w = 2(2+i)+(2+3i) = 2\cdot 2 + 2 + (2+3)i = 6+5i</math>}}
 +
 +
and we can mark this point on the complex plane.
 +
 +
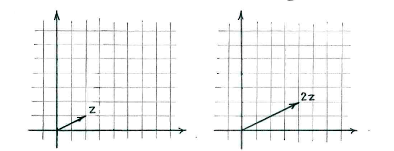
If we treat <math>z</math> and <math>w</math> as vectors, then <math>2z</math> is the vector which has the same direction as <math>z</math>, but is twice as long.
[[Image:3_2_1_c1.gif|center]]
[[Image:3_2_1_c1.gif|center]]
 +
 +
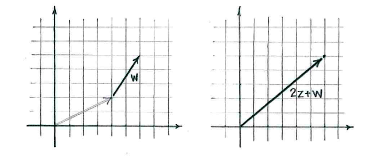
We add <math>w</math> to this vector and get <math>2z+w</math>.
[[Image:3_2_1_c2.gif|center]]
[[Image:3_2_1_c2.gif|center]]

Current revision

By calculation, we obtain

\displaystyle 2z+w = 2(2+i)+(2+3i) = 2\cdot 2 + 2 + (2+3)i = 6+5i

and we can mark this point on the complex plane.

If we treat \displaystyle z and \displaystyle w as vectors, then \displaystyle 2z is the vector which has the same direction as \displaystyle z, but is twice as long.

We add \displaystyle w to this vector and get \displaystyle 2z+w.

Retrieved from "http://wiki.sommarmatte.se/wikis/2008/bridgecourse2-ImperialCollege/index.php/Solution_3.2:1c"