From Förberedande kurs i matematik 2

Revision as of 07:59, 21 August 2008 (edit) Tekbot (Talk | contribs) m (Robot: Automated text replacement (-[[Bild: +[[Image:)) ← Previous diff		Current revision (09:18, 28 October 2008) (edit) (undo) Tek (Talk | contribs) m
(3 intermediate revisions not shown.)
Line 1:		Line 1:
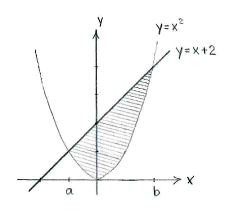
-	{{NAVCONTENT_START}}	+	The double inequality means that we look for the area of the region which is bounded above in the y-direction by the straight line <math>y=x+2</math> and from below by the parabola <math>y=x^2</math>.
-	<center> [[Image:2_1_4e-1(3).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	If we sketch the line and the parabola, the region is given by the region shaded in the figure below.
-	{{NAVCONTENT_START}}	+
-	<center> [[Image:2_1_4e-2(3).gif]] </center>	+	[[Image:2_1_4_e.gif|center]]
-	{{NAVCONTENT_STOP}}	+
-	{{NAVCONTENT_START}}	+	As soon as we have determined the ''x''-coordinates of the points of intersection,
-	<center> [[Image:2_1_4e-3(3).gif]] </center>	+	<math>x=a</math> and <math>x=b</math>, between the line and the parabola, we can calculate the area as the integral of the difference between the curves' ''y''-values,
-	{{NAVCONTENT_STOP}}	+
		+	{{Displayed math||<math>\text{Area} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{.}</math>}}
		+
		+	The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations
		+
		+	{{Displayed math||<math>\left\{\begin{align}
		+	y &= x+2\,,\\[5pt]
		+	y &= x^2\,\textrm{.}
		+	\end{align} \right.</math>}}
		+
		+	By eliminating <math>y</math>, we obtain an equation for <math>x</math>,
		+
		+	{{Displayed math||<math>x^{2}=x+2\,\textrm{.}</math>}}
		+
		+	If we move all ''x''-terms to the left-hand side,
		+
		+	{{Displayed math||<math>x^2-x=2\,,</math>}}
		+
		+	and complete the square, we obtain
		+
		+	{{Displayed math||<math>\begin{align}
		+	\Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt]
		+	\Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.}
		+	\end{align}</math>}}
		+
		+	Taking the root then gives that <math>x=\tfrac{1}{2}\pm \tfrac{3}{2}</math>. In other words, <math>x=-1</math> and <math>x=2\,</math>.
		+
		+	The area of the region is now given by
		+
		+	{{Displayed math||<math>\begin{align}
		+	\text{Area}
		+	&= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt]
		+	&= \Bigl[\ \frac{x^2}{2} + 2x - \frac{x^3}{3}\ \Bigr]_{-1}^2\\[5pt]
		+	&= \frac{2^2}{2} + 2\cdot 2 - \frac{2^3}{3} - \Bigl( \frac{(-1)^2}{2} + 2\cdot (-1) - \frac{(-1)^3}{3}\Bigr)\\[5pt]
		+	&= 2 + 4 - \frac{8}{3} - \frac{1}{2} + 2 - \frac{1}{3}\\[5pt]
		+	&= \frac{9}{2}\,\textrm{.}
		+	\end{align}</math>}}

---

Current revision

The double inequality means that we look for the area of the region which is bounded above in the y-direction by the straight line \displaystyle y=x+2 and from below by the parabola \displaystyle y=x^2.

If we sketch the line and the parabola, the region is given by the region shaded in the figure below.

As soon as we have determined the x-coordinates of the points of intersection, \displaystyle x=a and \displaystyle x=b, between the line and the parabola, we can calculate the area as the integral of the difference between the curves' y-values,

\displaystyle \text{Area} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{.}

The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations

\displaystyle \left\{\begin{align} y &= x+2\,,\\[5pt] y &= x^2\,\textrm{.} \end{align} \right.

By eliminating \displaystyle y, we obtain an equation for \displaystyle x,

\displaystyle x^{2}=x+2\,\textrm{.}

If we move all x-terms to the left-hand side,

\displaystyle x^2-x=2\,,

and complete the square, we obtain

\displaystyle \begin{align} \Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt] \Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.} \end{align}

Taking the root then gives that \displaystyle x=\tfrac{1}{2}\pm \tfrac{3}{2}. In other words, \displaystyle x=-1 and \displaystyle x=2\,.

The area of the region is now given by

\displaystyle \begin{align} \text{Area} &= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt] &= \Bigl[\ \frac{x^2}{2} + 2x - \frac{x^3}{3}\ \Bigr]_{-1}^2\\[5pt] &= \frac{2^2}{2} + 2\cdot 2 - \frac{2^3}{3} - \Bigl( \frac{(-1)^2}{2} + 2\cdot (-1) - \frac{(-1)^3}{3}\Bigr)\\[5pt] &= 2 + 4 - \frac{8}{3} - \frac{1}{2} + 2 - \frac{1}{3}\\[5pt] &= \frac{9}{2}\,\textrm{.} \end{align}