From Förberedande kurs i matematik 2

Revision as of 08:12, 21 August 2008 (edit) Tekbot (Talk | contribs) m (Robot: Automated text replacement (-[[Bild: +[[Image:)) ← Previous diff		Current revision (12:13, 30 October 2008) (edit) (undo) Tek (Talk | contribs) m
(3 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	The equation <math>z^3=-1</math> is a so-called binomial equation, which we solve by writing both sides in polar form. We have
-	<center> [[Image:3_3_2b-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{{Displayed math||<math>\begin{align}
-	{{NAVCONTENT_START}}	+	z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt]
-	<center> [[Image:3_3_2b-2(2).gif]] </center>	+	-1 &= 1\,(\cos\pi + i\sin\pi)\,,
-	{{NAVCONTENT_STOP}}	+	\end{align}</math>}}
		+
		+	and, with the help of de Moivre's formula, the equation becomes
		+
		+	{{Displayed math||<math>r^3(\cos 3\alpha + i\sin 3\alpha) = 1\,(\cos\pi + i\sin\pi)\,\textrm{.}</math>}}
		+
		+	Both sides are equal when their magnitudes are equal and the arguments differ by a multiple of <math>2\pi</math>,
		+
		+	{{Displayed math||<math>\left\{\begin{align}
		+	r^3 &= 1\,,\\[5pt]
		+	3\alpha &= \pi + 2n\pi\,,\quad\text{(n is an arbitrary integer),}
		+	\end{align}\right.</math>}}
		+
		+	which gives that
		+
		+	{{Displayed math||<math>\left\{\begin{align}
		+	r &= 1\,\\[5pt]
		+	\alpha &= \frac{\pi}{3}+\frac{2n\pi}{3}\quad\text{(n is an arbitrary integer).}
		+	\end{align}\right.</math>}}
		+
		+	For every third integer <math>n</math>, the solution formula gives in principal the same value for the argument (the difference is a multiple of <math>2\pi</math>), so the equation has in reality three solutions (for <math>n=0</math>, <math>1</math> and <math>\text{2}</math>),
		+
		+	{{Displayed math||<math>z=\left\{\begin{align}
		+	&1\cdot \Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\\[5pt]
		+	&1\cdot \Bigl(\cos\pi + i\sin\pi\Bigr)\\[5pt]
		+	&1\cdot \Bigl(\cos\frac{5\pi}{3} + i\sin\frac{5\pi}{3}\Bigr)
		+	\end{align}\right.
		+	=
		+	\left\{\begin{align}
		+	&\frac{1+i\sqrt{3}}{2}\,,\\[5pt]
		+	&-1\vphantom{\bigl(}\,,\\[5pt]
		+	&\frac{1-i\sqrt{3}}{2}\,\textrm{.}
		+	\end{align} \right.</math>}}
		+
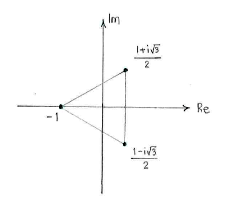
		+	We obtain the typical behaviour that the solutions are corner points in a regular polygon (a triangle in this case because the degree of the equation is 3.
		+
		+	[[Image:3_3_2_b.gif|center]]

---

Current revision

The equation \displaystyle z^3=-1 is a so-called binomial equation, which we solve by writing both sides in polar form. We have

\displaystyle \begin{align} z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] -1 &= 1\,(\cos\pi + i\sin\pi)\,, \end{align}

and, with the help of de Moivre's formula, the equation becomes

\displaystyle r^3(\cos 3\alpha + i\sin 3\alpha) = 1\,(\cos\pi + i\sin\pi)\,\textrm{.}

Both sides are equal when their magnitudes are equal and the arguments differ by a multiple of \displaystyle 2\pi,

\displaystyle \left\{\begin{align} r^3 &= 1\,,\\[5pt] 3\alpha &= \pi + 2n\pi\,,\quad\text{(n is an arbitrary integer),} \end{align}\right.

which gives that

\displaystyle \left\{\begin{align} r &= 1\,\\[5pt] \alpha &= \frac{\pi}{3}+\frac{2n\pi}{3}\quad\text{(n is an arbitrary integer).} \end{align}\right.

For every third integer \displaystyle n, the solution formula gives in principal the same value for the argument (the difference is a multiple of \displaystyle 2\pi), so the equation has in reality three solutions (for \displaystyle n=0, \displaystyle 1 and \displaystyle \text{2}),

\displaystyle z=\left\{\begin{align} &1\cdot \Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\\[5pt] &1\cdot \Bigl(\cos\pi + i\sin\pi\Bigr)\\[5pt] &1\cdot \Bigl(\cos\frac{5\pi}{3} + i\sin\frac{5\pi}{3}\Bigr) \end{align}\right. = \left\{\begin{align} &\frac{1+i\sqrt{3}}{2}\,,\\[5pt] &-1\vphantom{\bigl(}\,,\\[5pt] &\frac{1-i\sqrt{3}}{2}\,\textrm{.} \end{align} \right.

We obtain the typical behaviour that the solutions are corner points in a regular polygon (a triangle in this case because the degree of the equation is 3.