Solution 3.3:1a

From Förberedande kurs i matematik 2

(Difference between revisions)
Jump to: navigation, search
(Ny sida: {{NAVCONTENT_START}} <center> Bild:3_3_1a-1(2).gif </center> {{NAVCONTENT_STOP}} {{NAVCONTENT_START}} <center> Bild:3_3_1a-2(2).gif </center> {{NAVCONTENT_STOP}})
Current revision (08:50, 30 October 2008) (edit) (undo)
m
 
(4 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
Powers are repeated multiplications and because multiplication is a relatively simple arithmetical operation when it is carried out in polar form, calculating powers also becomes fairly simple in polar form,
-
<center> [[Bild:3_3_1a-1(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
{{Displayed math||<math>\bigl(r(\cos\alpha + i\sin\alpha)\bigr)^n = r^n(\cos n\alpha + i\sin n\alpha)\,\textrm{.}</math>}}
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Bild:3_3_1a-2(2).gif]] </center>
+
The equation above is called de Moivre's formula.
-
{{NAVCONTENT_STOP}}
+
 
 +
The plan is therefore to rewrite <math>1+i</math> in polar form, raise the expression to the power <math>12</math> using de Moivre's formula and then to write the answer in the form <math>a+ib</math>.
 +
 
 +
<center>[[Image:3_3_1_a1.gif]] [[Image:3_3_1_a_text.gif]]</center>
 +
 
 +
Using the calculations above, we see that
 +
 
 +
{{Displayed math||<math>1+i = \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4} \Bigr)\,\textrm{.}</math>}}
 +
 
 +
De Moivre's formula now gives
 +
 
 +
{{Displayed math||<math>\begin{align}
 +
(1+i)^{12}
 +
&= \bigl(\sqrt{2}\,\bigr)^{12}\Bigl(\cos \Bigl(12\cdot\frac{\pi}{4}\Bigr) + i\sin \Bigl(12\cdot\frac{\pi}{4}\Bigr)\Bigr)\\[5pt]
 +
&= 2^{(1/2)\cdot 12}\Bigl(\cos 3\pi + i\sin 3\pi\Bigr)\\[5pt]
 +
&= 2^6(-1+i\cdot 0)\\[5pt]
 +
&= 64\cdot (-1)\\[5pt]
 +
&= -64\,\textrm{.}
 +
\end{align}</math>}}

Current revision

Powers are repeated multiplications and because multiplication is a relatively simple arithmetical operation when it is carried out in polar form, calculating powers also becomes fairly simple in polar form,

\displaystyle \bigl(r(\cos\alpha + i\sin\alpha)\bigr)^n = r^n(\cos n\alpha + i\sin n\alpha)\,\textrm{.}

The equation above is called de Moivre's formula.

The plan is therefore to rewrite \displaystyle 1+i in polar form, raise the expression to the power \displaystyle 12 using de Moivre's formula and then to write the answer in the form \displaystyle a+ib.

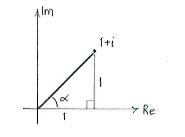
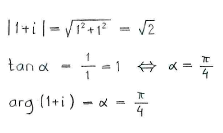
Image:3_3_1_a1.gif Image:3_3_1_a_text.gif

Using the calculations above, we see that

\displaystyle 1+i = \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4} \Bigr)\,\textrm{.}

De Moivre's formula now gives

\displaystyle \begin{align}

(1+i)^{12} &= \bigl(\sqrt{2}\,\bigr)^{12}\Bigl(\cos \Bigl(12\cdot\frac{\pi}{4}\Bigr) + i\sin \Bigl(12\cdot\frac{\pi}{4}\Bigr)\Bigr)\\[5pt] &= 2^{(1/2)\cdot 12}\Bigl(\cos 3\pi + i\sin 3\pi\Bigr)\\[5pt] &= 2^6(-1+i\cdot 0)\\[5pt] &= 64\cdot (-1)\\[5pt] &= -64\,\textrm{.} \end{align}

Retrieved from "http://wiki.sommarmatte.se/wikis/2008/bridgecourse2-ImperialCollege/index.php/Solution_3.3:1a"