Solution 3.2:2c
From Förberedande kurs i matematik 2
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
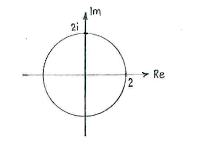
| - | + | The magnitude <math>|z|</math> of a complex number <math>z</math> is equal to the number's distance from the origin. The condition <math>|z|=2</math> therefore says that <math>z</math>'s distance from the origin should be 2, i.e. the condition gives a circle of radius 2 and centre at the origin. | |
| - | The magnitude <math>|z|</math> of a complex number <math>z</math> is equal to the number's distance from the origin. The condition <math>|z|=2</math> therefore says that <math>z</math>'s distance from the origin should be | + | |
[[Image:3_2_2_c_.gif|center]] | [[Image:3_2_2_c_.gif|center]] | ||
| - | |||
| - | {{NAVCONTENT_STOP}} | ||
Current revision
The magnitude \displaystyle |z| of a complex number \displaystyle z is equal to the number's distance from the origin. The condition \displaystyle |z|=2 therefore says that \displaystyle z's distance from the origin should be 2, i.e. the condition gives a circle of radius 2 and centre at the origin.