Solution 2.2:2a

From Förberedande kurs i matematik 2

(Difference between revisions)
Jump to: navigation, search
m (Lösning 2.2:2a moved to Solution 2.2:2a: Robot: moved page)
Current revision (12:57, 28 October 2008) (edit) (undo)
m
 
(One intermediate revision not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The integral is a standard integral, with <math>5x</math> as the argument of the cosine function. If we therefore substitute <math>u=5x</math>, we obtain the “correct” argument of the cosine,
-
<center> [[Image:2_2_2a-1(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
-
{{NAVCONTENT_START}}
+
-
<center> [[Image:2_2_2a-2(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
 +
{{Displayed math||<math>\int\limits_0^{\pi} \cos 5x\,dx = \left\{\begin{align}
 +
u &= 5x\\[5pt]
 +
du &= (5x)'\,dx = 5\,dx
 +
\end{align}\right\} = \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du\,\textrm{.}</math>}}
 +
 +
As can be seen, the variable change replaced <math>dx</math> by <math>\tfrac{1}{5}\,du</math> and the new limits of integration become <math>u=5\cdot 0=0</math>
 +
and <math>u=5\cdot \pi = 5\pi\,</math>.
 +
 +
Now, we have a standard integral which we can easily compute,
 +
 +
{{Displayed math||<math>\frac{1}{5}\int\limits_0^{5\pi} \cos u\,du = \frac{1}{5}\Bigl[\ \sin u\ \Bigr]_0^{5\pi} = \frac{1}{5}( \sin 5\pi -\sin 0) = \frac{1}{5}(0-0) = 0\,\textrm{.}</math>}}
 +
 +
 +
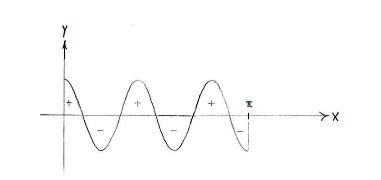
Note: If we draw the graph of <math>y=\cos 5x</math>, we see also that the area between the curve and ''x''-axis above the ''x''-axis is the same as the area under the ''x''-axis.
[[Image:2_2_2_a.gif|center]]
[[Image:2_2_2_a.gif|center]]

Current revision

The integral is a standard integral, with \displaystyle 5x as the argument of the cosine function. If we therefore substitute \displaystyle u=5x, we obtain the “correct” argument of the cosine,

\displaystyle \int\limits_0^{\pi} \cos 5x\,dx = \left\{\begin{align}

u &= 5x\\[5pt] du &= (5x)'\,dx = 5\,dx \end{align}\right\} = \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du\,\textrm{.}

As can be seen, the variable change replaced \displaystyle dx by \displaystyle \tfrac{1}{5}\,du and the new limits of integration become \displaystyle u=5\cdot 0=0 and \displaystyle u=5\cdot \pi = 5\pi\,.

Now, we have a standard integral which we can easily compute,

\displaystyle \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du = \frac{1}{5}\Bigl[\ \sin u\ \Bigr]_0^{5\pi} = \frac{1}{5}( \sin 5\pi -\sin 0) = \frac{1}{5}(0-0) = 0\,\textrm{.}


Note: If we draw the graph of \displaystyle y=\cos 5x, we see also that the area between the curve and x-axis above the x-axis is the same as the area under the x-axis.

Retrieved from "http://wiki.sommarmatte.se/wikis/2008/bridgecourse2-ImperialCollege/index.php/Solution_2.2:2a"