Solution 1.3:2b

From Förberedande kurs i matematik 2

(Difference between revisions)
Jump to: navigation, search
Current revision (12:46, 17 October 2008) (edit) (undo)
m
 
(3 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
In order to determine the function's extreme points, we investigate three types of points,
-
<center> [[Bild:1_3_2b-1(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
-
{{NAVCONTENT_START}}
+
-
<center> [[Bild:1_3_2b-2(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
-
[[Bild:1_3_2_b.gif|center]]
+
# critical points, i.e. where <math>f^{\,\prime}(x)=0</math>,
 +
# points where the function is not differentiable, and
 +
# endpoints of the interval of definition.
 +
 +
In our case, we have that:
 +
 
 +
<ol>
 +
<li>The derivative of <math>f(x)</math> is given by
 +
{{Displayed math||<math>f^{\,\prime}(x) = 3-2x</math>}}
 +
and becomes zero when <math>x=3/2\,</math>.</li>
 +
 
 +
<li>The function is a polynomial, and is therefore differentiable everywhere.</li>
 +
 
 +
<li>The function is defined for all ''x'', and therefore the interval of definition has no endpoints.</li>
 +
</ol>
 +
 
 +
There is thus just one point <math>x=3/2\,</math>, where the function possibly has an extreme point.
 +
 
 +
If we write down a sign table for the derivative, we see that <math>x=3/2</math> is a local maximum.
 +
 
 +
 
 +
{| border="1" cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
|width="50px" align="center" style="background:#efefef;"| <math>x</math>
 +
|width="50px" align="center" style="background:#efefef;"|
 +
|width="50px" align="center" style="background:#efefef;"| <math>\tfrac{3}{2}</math>
 +
|width="50px" align="center" style="background:#efefef;"|
 +
|-
 +
|width="50px" align="center"| <math>f^{\,\prime}(x)</math>
 +
|width="50px" align="center"| <math>+</math>
 +
|width="50px" align="center"| <math>0</math>
 +
|width="50px" align="center"| <math>-</math>
 +
|-
 +
|width="50px" align="center"| <math>f(x)</math>
 +
|width="50px" align="center"| <math>\nearrow</math>
 +
|width="50px" align="center"| <math>\tfrac{17}{4}</math>
 +
|width="50px" align="center"| <math>\searrow</math>
 +
|}
 +
 
 +
 
 +
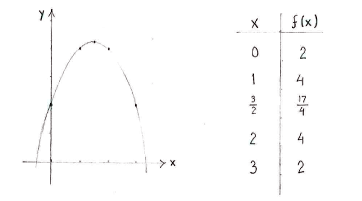
Because the function is given by a second-degree expression, its graph is a parabola with a maximum at <math>(3/2, 17/4)</math> and we can draw it with the help of a few couple of points.
 +
 
 +
[[Image:1_3_2_b.gif||center]]

Current revision

In order to determine the function's extreme points, we investigate three types of points,

  1. critical points, i.e. where \displaystyle f^{\,\prime}(x)=0,
  2. points where the function is not differentiable, and
  3. endpoints of the interval of definition.

In our case, we have that:

  1. The derivative of \displaystyle f(x) is given by
    \displaystyle f^{\,\prime}(x) = 3-2x
    and becomes zero when \displaystyle x=3/2\,.
  2. The function is a polynomial, and is therefore differentiable everywhere.
  3. The function is defined for all x, and therefore the interval of definition has no endpoints.

There is thus just one point \displaystyle x=3/2\,, where the function possibly has an extreme point.

If we write down a sign table for the derivative, we see that \displaystyle x=3/2 is a local maximum.


\displaystyle x \displaystyle \tfrac{3}{2}
\displaystyle f^{\,\prime}(x) \displaystyle + \displaystyle 0 \displaystyle -
\displaystyle f(x) \displaystyle \nearrow \displaystyle \tfrac{17}{4} \displaystyle \searrow


Because the function is given by a second-degree expression, its graph is a parabola with a maximum at \displaystyle (3/2, 17/4) and we can draw it with the help of a few couple of points.

Retrieved from "http://wiki.sommarmatte.se/wikis/2008/bridgecourse2-ImperialCollege/index.php/Solution_1.3:2b"