From Förberedande kurs i matematik 2

Revision as of 13:37, 19 August 2008 (edit) Per (Talk | contribs) ← Previous diff		Current revision (12:05, 17 October 2008) (edit) (undo) Tek (Talk | contribs) m
(3 intermediate revisions not shown.)
Line 1:		Line 1:
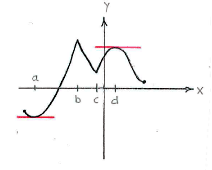
-	{{NAVCONTENT_START}}	+	The function has critical points at the points <math>x=a</math> and <math>x=d</math>, (see figure below), i.e. the derivatives are equal to zero, but note that <math>x=b</math> and <math>x=c</math> are not critical points (the derivative is not even defined at these points).
-	<center> [[Bild:1_3_1d-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
-	{{NAVCONTENT_START}}	+
-	<center> [[Bild:1_3_1d-2(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
-	[[Bild:1_3_1_d1.gif|center]]	+	[[Image:1_3_1_d1.gif|center]]
-	[[Bild:1_3_1_d2.gif|center]]	+
		+	The function has local minimum points at <math>x=a</math>, <math>x=c</math> and the right endpoint of the interval of definition and the local maximum points at the left endpoint, <math>x=b</math>, and <math>x=d</math>. Of these, <math>x=b</math> is the global maximum and <math>x=a</math> is the global minimum.
		+
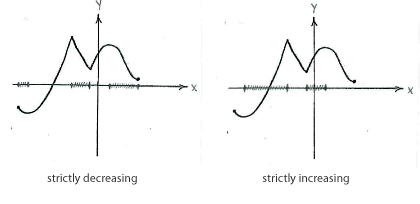
		+	Between the local extreme points, the function is strictly increasing or decreasing.
		+
		+	[[Image:1_3_1_d2.gif|center]]

---

Current revision

The function has critical points at the points \displaystyle x=a and \displaystyle x=d, (see figure below), i.e. the derivatives are equal to zero, but note that \displaystyle x=b and \displaystyle x=c are not critical points (the derivative is not even defined at these points).

The function has local minimum points at \displaystyle x=a, \displaystyle x=c and the right endpoint of the interval of definition and the local maximum points at the left endpoint, \displaystyle x=b, and \displaystyle x=d. Of these, \displaystyle x=b is the global maximum and \displaystyle x=a is the global minimum.

Between the local extreme points, the function is strictly increasing or decreasing.