Solution 1.1:1a
From Förberedande kurs i matematik 2
(Difference between revisions)
m (Robot: Automated text replacement (-[[Bild: +[[Image:)) |
|||
| Line 1: | Line 1: | ||
{{NAVCONTENT_START}} | {{NAVCONTENT_START}} | ||
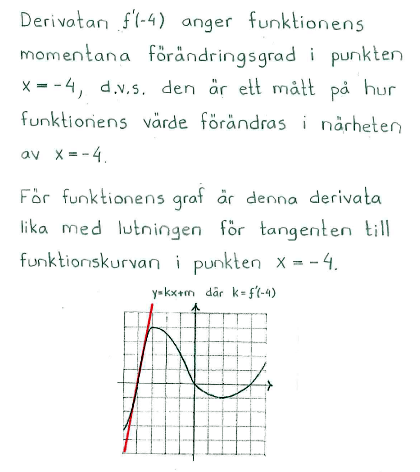
| + | The derivative f'(-4)gives the function's instantaneous rate of change at the point x=-4, i.e. it is a measure of the function's value changes in the vicinity of x=-4. | ||
| + | |||
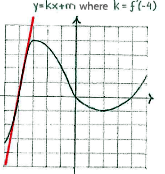
| + | In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point x=-4. | ||
| + | |||
| + | [[Image:1_1_1_a1.gif|center]] | ||
| + | |||
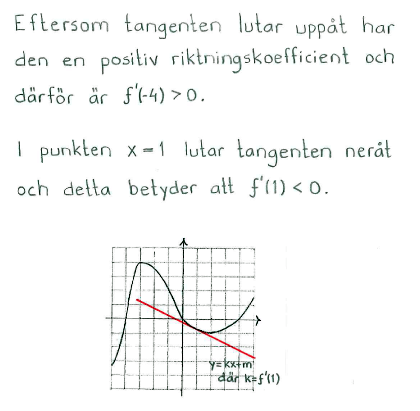
| + | Because the tangent is sloping upwards, it has a positive gradient and therefore f'(-4)>0. | ||
| + | |||
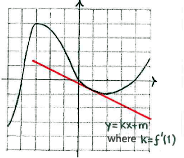
| + | At the point x=1, the tangent slopes downwards and this means that f'(1)<0. | ||
| + | |||
| + | [[Image:1_1_1_a2.gif|center]] | ||
| + | |||
| + | |||
<center> [[Image:1_1_1a-1(2).gif]] </center> | <center> [[Image:1_1_1a-1(2).gif]] </center> | ||
{{NAVCONTENT_STOP}} | {{NAVCONTENT_STOP}} | ||
| Line 5: | Line 18: | ||
<center> [[Image:2_1_1a-2(2).gif]] </center> | <center> [[Image:2_1_1a-2(2).gif]] </center> | ||
{{NAVCONTENT_STOP}} | {{NAVCONTENT_STOP}} | ||
| - | |||
| - | [[Image:1_1_1_a1.gif|center]] | ||
| - | |||
| - | [[Image:1_1_1_a2.gif|center]] | ||
Revision as of 15:24, 5 September 2008
The derivative f'(-4)gives the function's instantaneous rate of change at the point x=-4, i.e. it is a measure of the function's value changes in the vicinity of x=-4.
In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point x=-4.
Because the tangent is sloping upwards, it has a positive gradient and therefore f'(-4)>0.
At the point x=1, the tangent slopes downwards and this means that f'(1)<0.