Solution 4.4:5b
From Förberedande kurs i matematik 1
Let's first investigate when the equality
\displaystyle \tan u=\tan v
is satisfied. Because
\displaystyle u
can be interpreted as the slope (gradient) of the line which makes an angle
\displaystyle u
with the positive
\displaystyle x
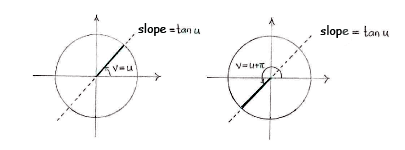
-axis, we see that for a fixed value of tan u, there are two angles
\displaystyle v
in the unit circle with this slope:
\displaystyle v=u
and
\displaystyle v=u+\pi
slope \displaystyle =\text{ tan }u slope \displaystyle =\text{ tan }u
The angle
\displaystyle v
has the same slope after every half turn, so if we add multiples of
\displaystyle \pi \text{ }
to
\displaystyle u, we will obtain all the angles
\displaystyle v
which satisfy the equality
\displaystyle v=u+n\pi
where
\displaystyle n
is an arbitrary integer.
If we apply this result to the equation
\displaystyle \tan x=\tan 4x
we see that the solutions are given by
\displaystyle 4x=x+n\pi
(
\displaystyle n
an arbitrary integer),
and solving for \displaystyle x gives
\displaystyle x=\frac{1}{3}n\pi
(
\displaystyle n
an arbitrary integer).