From Förberedande kurs i matematik 1

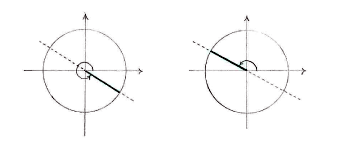
A quick sketch of the unit circle and the line \displaystyle y=-\frac{1}{\sqrt{3}}x, which corresponds to the tangent value \displaystyle -{1}/{\sqrt{3}}\; shows that there are two angles which satisfy \displaystyle \tan v=-{1}/{\sqrt{3}}\;. One of the angles lies in the fourth quadrant and the other is the opposite angle in the second quadrant.

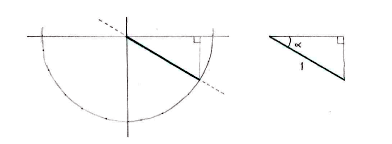
We can therefore limit ourselves to the fourth quadrant and draw an auxiliary triangle in order to determine the angle there.

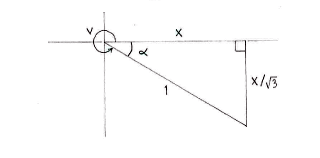
If we call \displaystyle x the side adjacent to the angle \displaystyle \alpha then the fact that \displaystyle \tan v=-{1}/{\sqrt{3}}\; gives the length of the opposite side as \displaystyle {x}/{\sqrt{3}}\;.

Pythagoras' theorem gives

\displaystyle x^{2}+\left( \frac{x}{\sqrt{3}} \right)^{2}=1^{2}

and this equation has the solution \displaystyle x={\sqrt{3}}/{2}\;, which means that

\displaystyle \cos \alpha =\frac{{\sqrt{3}}/{2}\;}{1}=\frac{\sqrt{3}}{2}

i.e. \displaystyle \alpha ={\pi }/{6}\;. Because the angle \displaystyle v in the fourth quadrant is the complement of \displaystyle \alpha

\displaystyle v is given by

\displaystyle v=2\pi -\alpha =2\pi -\frac{\pi }{6}=\frac{11\pi }{6}. If we subtract half a turn, \displaystyle \pi , we obtain the other angle

\displaystyle v=\frac{11\pi }{6}-\pi =\frac{5\pi }{6}