Solution 4.2:9

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (12:46, 9 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
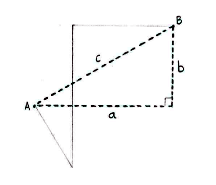
If we introduce the dashed triangle below, the distance as the crow flies between
+
If we introduce the dashed triangle below, the distance as the crow flies between A and B is equal to the triangle's hypotenuse, ''c''.
-
<math>\text{A}</math>
+
-
and
+
-
<math>\text{B}</math>
+
-
is equal to the triangle's hypotenuse,
+
-
<math>c</math>.
+
-
 
+
[[Image:4_2_9_1.gif|center]]
[[Image:4_2_9_1.gif|center]]
-
One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since Pythagoras' theorem then gives
+
One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since the Pythagorean theorem then gives
 +
{{Displayed math||<math>c^2 = a^2 + b^2\,\textrm{.}</math>}}
-
<math>c^{2}=a^{2}+b^{2}</math>
+
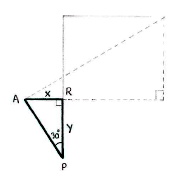
In turn, we can determine the opposite and adjacent by introducing another triangle APR, where R is the point on the line PQ which the dashed triangle's side of length ''a'' cuts the line.
-
 
+
-
 
+
-
In turn, we can determine the opposite and adjacent by introducing another triangle
+
-
<math>\text{APR}</math>, where
+
-
<math>\text{R}</math>
+
-
is the point on the line
+
-
<math>\text{PQ}</math>
+
-
which the dashed triangle's side of length
+
-
<math>a</math>
+
-
cuts the line.
+
[[Image:4_2_9_2.gif|center]]
[[Image:4_2_9_2.gif|center]]
-
Because we know that
+
Because we know that <math>\text{AP}=4</math> and the angle at P, simple trigonometry shows that ''x'' and ''y'' are given by
-
<math>\text{AP}=\text{4}</math>
+
-
and the angle at P, simple trigonometry shows that
+
-
<math>x</math>
+
-
and
+
-
<math>y</math>
+
-
are given by
+
-
 
+
-
 
+
-
<math>\begin{align}
+
-
& x=4\sin 30^{\circ }=4\centerdot \frac{1}{2}=2, \\
+
-
& y=4\cos 30^{\circ }=4\centerdot \frac{\sqrt{3}}{2}=2\sqrt{3} \\
+
-
\end{align}</math>
+
-
 
+
-
 
+
-
We can now start to look for the solution. Since
+
-
<math>x</math>
+
-
and
+
-
<math>y</math>
+
-
have been calculated, we can determine
+
-
<math>a</math>
+
-
and b by considering the horizontal and vertical distances in the figure.
+
-
 
+
-
 
+
-
[[Image:4_2_9_3.gif|center]]
+
-
<math>a=x+5=2+5=7</math>
+
{{Displayed math||<math>\begin{align}
-
+
x &= 4\sin 30^{\circ } = 4\cdot \frac{1}{2} = 2,\\[5pt]
-
<math>b=12-y=12-2\sqrt{3}</math>
+
y &= 4\cos 30^{\circ } = 4\cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}\,\textrm{.}
 +
\end{align}</math>}}
 +
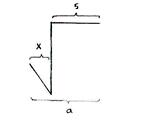
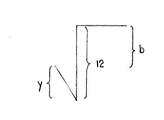
We can now start to look for the solution. Since ''x'' and ''y'' have been calculated, we can determine ''a'' and ''b'' by considering the horizontal and vertical distances in the figure.
-
With a and
+
{| align="center"
-
<math>b</math>
+
| align="center" |[[Image:4_2_9_3-1.gif]]
-
given, Pythagoras' theorem leads to
+
| width="20px"|&nbsp;
 +
| align="center" |[[Image:4_2_9_3-2.gif]]
 +
|-
 +
| align="center" valign="top"|<math>\begin{align}a &= x+5\\ &= 2+5 = 7\end{align}</math>
 +
||
 +
| align="center" valign="top"|<math>\begin{align}b &= 12-y\\ &= 12-2\sqrt{3}\end{align}</math>
 +
|}
 +
With ''a'' and ''b'' given, the Pythagorean theorem leads to
-
<math>\begin{align}
+
{{Displayed math||<math>\begin{align}
-
& c=\sqrt{a^{2}+b^{2}}=\sqrt{7^{2}+\left( 12-2\sqrt{3} \right)^{2}} \\
+
c &= \sqrt{a^2+b^2}\\[5pt]
-
& =\sqrt{49+\left( 12^{2}-2\centerdot 12\centerdot 2\sqrt{3}+\left( 2\sqrt{3} \right)^{2} \right)} \\
+
&= \sqrt{7^2+(12-2\sqrt{3})^2}\\[5pt]
-
& =\sqrt{205-38\sqrt{3}}\quad \approx \quad 11.0\quad \text{km}\text{.} \\
+
&= \sqrt{49+(12^2-2\cdot 12\cdot 2\sqrt{3}+(2\sqrt{3})^2)}\\[5pt]
-
\end{align}</math>
+
&= \sqrt{205-38\sqrt{3}}\\[5pt]
 +
&\approx 11\textrm{.}0\ \text{km}\textrm{.}
 +
\end{align}</math>}}

Current revision

If we introduce the dashed triangle below, the distance as the crow flies between A and B is equal to the triangle's hypotenuse, c.

One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since the Pythagorean theorem then gives

\displaystyle c^2 = a^2 + b^2\,\textrm{.}

In turn, we can determine the opposite and adjacent by introducing another triangle APR, where R is the point on the line PQ which the dashed triangle's side of length a cuts the line.

Because we know that \displaystyle \text{AP}=4 and the angle at P, simple trigonometry shows that x and y are given by

\displaystyle \begin{align}

x &= 4\sin 30^{\circ } = 4\cdot \frac{1}{2} = 2,\\[5pt] y &= 4\cos 30^{\circ } = 4\cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}\,\textrm{.} \end{align}

We can now start to look for the solution. Since x and y have been calculated, we can determine a and b by considering the horizontal and vertical distances in the figure.

Image:4_2_9_3-1.gif   Image:4_2_9_3-2.gif
\displaystyle \begin{align}a &= x+5\\ &= 2+5 = 7\end{align} \displaystyle \begin{align}b &= 12-y\\ &= 12-2\sqrt{3}\end{align}

With a and b given, the Pythagorean theorem leads to

\displaystyle \begin{align}

c &= \sqrt{a^2+b^2}\\[5pt] &= \sqrt{7^2+(12-2\sqrt{3})^2}\\[5pt] &= \sqrt{49+(12^2-2\cdot 12\cdot 2\sqrt{3}+(2\sqrt{3})^2)}\\[5pt] &= \sqrt{205-38\sqrt{3}}\\[5pt] &\approx 11\textrm{.}0\ \text{km}\textrm{.} \end{align}

Retrieved from "http://wiki.sommarmatte.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.2:9"