Solution 4.1:10

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (13:34, 8 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
{{NAVCONTENT_START}}
 
-
<center> [[Image:4_1_10-1(5)_.gif]] </center>
 
- 
-
{{NAVCONTENT_STOP}}
 
- 
- 
- 
- 
First, let's decide to determine all distance in dm (decimeters), so that we have all the distances as integers.
First, let's decide to determine all distance in dm (decimeters), so that we have all the distances as integers.
-
Call the length of the washing line from the trees to the hanger
+
Call the length of the washing line from the trees to the hanger ''y'' and ''z'', as in the figure below, and introduce two auxiliary triangles which have ''y'' and ''z'' as their hypotenuses. (As an approximation, we suppose that the taut washing line consists of two straight parts.)
-
<math>y</math>
+
-
and
+
-
<math>z</math>, as in the figure below, and introduce two auxiliary triangles which have
+
-
<math>y</math>
+
-
and
+
-
<math>z</math>
+
-
as their hypotenuses. (As an approximation, we suppose that the taut washing line consists of two straight parts.)
+
-
Because the line is
 
-
<math>\text{54}</math>
 
-
dm long, we have
 
 +
<center> [[Image:4_1_10-1(5)_.gif]] </center>
-
<math>y+z=54</math>
 
-
(1)
 
-
Then, Pythagoras' theorem gives the relations
+
Because the line is 54 dm long, we have
 +
{{Displayed math||<math>y+z=54\,\textrm{.}</math>|(1)}}
-
<math>y^{2}=x^{2}+12^{2}</math>
+
Then, the Pythagorean theorem gives the relations
-
(2)
+
-
<math>z^{2}=\left( x+6 \right)^{2}+36^{2}</math>
+
{{Displayed math||<math>y^2 = x^2 + 12^2\,,</math>|(2)}}
-
(3)
+
{{Displayed math||<math>z^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3)}}
 +
The idea now is to solve the system of equations (1)-(3) by first eliminating ''z'', so that we get two equations which only contain ''x'' and ''y''. Then, eliminate ''y'' from one of these equations, so that we get an equation which determines ''x''.
-
The idea now is to solve the equation system (1)-(3) by first eliminating
+
From (1), we have <math>z = 54-y</math>, and substituting this into (3) gives us the equation
-
<math>z</math>, so that we get two equations which only contain
+
-
<math>x</math>
+
-
and
+
-
<math>y</math>. Then, eliminate
+
-
<math>y</math>
+
-
from one of these equations, so that we get an equation which determines
+
-
<math>x</math>.
+
-
From (1), we have
+
{{Displayed math||<math>(54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3')}}
-
<math>z=\text{54}-y</math>, and substituting this into (3) gives us the equation
+
 +
Equations (2) and (3') together give a smaller system for ''x'' and ''y'',
-
<math>\left( \text{54}-y \right)^{2}=\left( x+6 \right)^{2}+36^{2}</math>
+
{{Displayed math||<math>\left\{ \begin{align}
-
(3')
+
& y^2 = x^2 + 12^2\,,\\[5pt]
 +
& (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}
 +
\end{align} \right.</math>|<math>\begin{align}(2)\\[5pt] (3')\end{align}</math>}}
-
Equations (2) and (3') together give a smaller equation system for
+
Expand the quadratic terms on both sides of (3'),
-
<math>x</math>
+
-
and
+
-
<math>y</math>:
+
-
 
+
-
 
+
-
 
+
-
<math>\left\{ \begin{align}
+
-
& y^{2}=x^{2}+12^{2}\quad \quad \quad \quad \quad \quad \quad (2) \\
+
-
& \left( \text{54}-y \right)^{2}=\left( x+6 \right)^{2}+36^{2}\quad \quad \left( \text{3}' \right) \\
+
-
\end{align} \right.</math>
+
-
 
+
-
+
-
 
+
-
 
+
-
Expand the quadratic terms on both sides of (3')
+
-
 
+
-
 
+
-
<math>54^{2}-2\centerdot 54\centerdot y+y^{2}=x^{2}+2\centerdot 6\centerdot x+6^{2}+36^{2}</math>
+
 +
{{Displayed math||<math>54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,</math>}}
and simplify
and simplify
 +
{{Displayed math||<math>2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}</math>}}
-
<math>2916-108y+y^{2}=x^{2}+12x+1332</math>
+
Use (2) and replace <math>y^2</math> with <math>x^2+12</math> in this equation,
 +
{{Displayed math||<math>2916 - 108y + x^2 + 144 = x^2 + 12x + 1332</math>}}
-
Use (2) and replace
+
which gets rid of the ''x''²-term,
-
<math>y^{\text{2}}</math>
+
-
with
+
-
<math>x^{\text{2}}+\text{12 }</math>
+
-
in this equation,
+
-
 
+
-
 
+
-
<math>2916-108y+x^{2}+144=x^{2}+12x+1332</math>
+
-
 
+
-
 
+
-
which gets rid of the
+
-
<math>x^{\text{2}}\text{ }</math>
+
-
term ,
+
-
 
+
-
 
+
-
<math>2916-108y+144=12x+1332</math>
+
 +
{{Displayed math||<math>2916 - 108y + 144 = 12x + 1332\,,</math>}}
and further simplification gives the equation
and further simplification gives the equation
 +
{{Displayed math||<math>12x + 108y = 1728</math>|(3")}}
-
<math>12x+108y=1728\quad \quad \quad \quad \quad \left( \text{3}'' \right)</math>
+
If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear
 +
{{Displayed math||<math>\left\{ \begin{align}
 +
& y^2 = x^2 + 12^2\,,\\[5pt]
 +
& 12x+108y=1728\,\textrm{.}
 +
\end{align} \right.</math>|<math>\begin{align}(2)\\[5pt] (3")\end{align}</math>}}
-
If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and
+
In this system, we can make ''y'' the subject in (3"),
-
<math>\left( \text{3}'' \right)</math>, where one of the equations is linear
+
 +
{{Displayed math||<math>y=\frac{1728-12x}{108}=16-\frac{x}{9}</math>}}
-
<math>\left\{ \begin{align}
+
and substitute into (2),
-
& y^{2}=x^{2}+12^{2}\quad \quad \quad \quad \quad \quad \quad (2) \\
+
-
& 12x+108y=1728\quad \quad \quad \quad \quad \left( \text{3}'' \right) \\
+
-
\end{align} \right.</math>
+
 +
{{Displayed math||<math>\Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}</math>}}
-
 
+
This is an equation which only contains ''x'', and if we solve it, we will get our answer.
-
In this system, we can make
+
-
<math>y\text{ }</math>
+
-
the subject in
+
-
<math>\left( \text{3}'' \right)</math>,
+
-
 
+
-
 
+
-
<math>y=\frac{1728-12x}{108}=16-\frac{x}{9}</math>
+
-
 
+
-
 
+
-
and substitute into (2):
+
-
 
+
-
 
+
-
<math>\left( 16-\frac{x}{9} \right)^{2}=x^{2}+144</math>
+
-
 
+
-
 
+
-
This is an equation which only contains
+
-
<math>x</math>, and if we solve it, we will get our answer.
+
Expand the quadratic on the left-hand side,
Expand the quadratic on the left-hand side,
-
 
+
{{Displayed math||<math>16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144</math>}}
-
<math>16^{2}-2\centerdot 16\centerdot \frac{x}{9}+\left( \frac{x}{9} \right)^{2}=x^{2}+144</math>
+
-
 
+
-
 
+
and collect together all terms on one side,
and collect together all terms on one side,
-
 
+
{{Displayed math||<math>x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,</math>}}
-
<math>\begin{align}
+
-
& x^{2}-\frac{x^{2}}{81}+\frac{32}{9}x+144-16^{2}=0 \\
+
-
& \\
+
-
\end{align}</math>
+
which gives the equation
which gives the equation
 +
{{Displayed math||<math>\frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}</math>}}
-
<math>\frac{80}{81}x^{2}+\frac{32}{9}x-112=0</math>
+
Multiply both sides by <math>81/80</math> so that we get the equation in standard form,
-
 
+
-
 
+
-
Multiply both sides by
+
-
<math>\frac{81}{80}</math>
+
-
so that we get the equation in standard form,
+
-
 
+
-
 
+
-
<math>x^{2}+\frac{18}{5}x-\frac{567}{5}=0</math>
+
 +
{{Displayed math||<math>x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}</math>}}
Completing the square on the left-hand side gives
Completing the square on the left-hand side gives
-
 
+
{{Displayed math||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0</math>}}
-
<math>\left( x+\frac{9}{5} \right)^{2}-\left( \frac{9}{5} \right)^{2}-\frac{567}{5}=0</math>
+
and then
and then
-
 
+
{{Displayed math||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,</math>}}
-
<math>\left( x+\frac{9}{5} \right)^{2}=\frac{81}{25}+\frac{567}{5}=\frac{2916}{25}</math>
+
-
 
+
i.e.
i.e.
-
 
+
{{Displayed math||<math>x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}</math>}}
-
<math>x=-\frac{9}{5}\pm \sqrt{\frac{2916}{25}}=-\frac{9}{5}\pm \frac{54}{5}</math>
+
-
 
+
This means that the equation has the solutions
This means that the equation has the solutions
 +
{{Displayed math||<math>x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}</math>}}
-
<math>x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}</math>
+
The answer is thus <math>x=9\ \textrm{dm}</math> (the negative root must be discarded).
-
and
+
-
<math>x=-\frac{9}{5}+\frac{54}{5}=9</math>
 
 +
To be sure that we have calculated correctly, we also look at the values of ''y'' and ''z'', and check that the original equations (1) to (3) are satisfied.
-
The answer is thus
+
Equation (3") gives
-
<math>x=\text{9 }</math>
+
-
dm (the negative root must be discarded).
+
-
 
+
-
To be sure that we have calculated correctly, we also look at the values of
+
-
<math>y</math>
+
-
and
+
-
<math>z</math>, and check that the original equations (1) to (3) are satisfied.
+
-
 
+
-
Equation (3'') gives
+
-
 
+
-
 
+
-
<math>y=16-\frac{x}{9}=16-1=15</math>
+
 +
{{Displayed math||<math>y = 16-\frac{x}{9} = 16-1 = 15</math>}}
and equation (1) gives
and equation (1) gives
 +
{{Displayed math||<math>z=54-y=54-15=39\,\textrm{.}</math>}}
-
<math>z=54-y=54-15=39</math>
+
Now, we check that <math>x=9</math>, <math>y=15</math> and <math>z=39</math> satisfy the equations (1), (2) and (3),
-
 
+
-
 
+
-
Now, we check that x=9,
+
-
<math>y</math>
+
-
=15 and z=39 satisfy the equations (1),(12) and (3).
+
-
 
+
-
LHS of (1)
+
-
<math>=15+39=54</math>
+
-
 
+
-
RHS of (1)
+
-
<math>=54</math>
+
-
 
+
-
LHS of (2)
+
-
<math>=15^{2}=225</math>
+
-
 
+
-
RHS of (2)
+
-
<math>=9^{2}+12^{2}=81+144=225</math>
+
-
 
+
-
LHS of (3)
+
-
<math>=39^{2}=1521</math>
+
-
RHS of (3)
+
{{Displayed math||<math>\begin{align}
-
<math>=\left( 9+6 \right)^{2}+36^{2}=15^{2}+36^{2}=225+1296=1521</math>
+
\textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt]
 +
\textrm{RHS of (1)} &= 54\,,\\[10pt]
 +
\textrm{LHS of (2)} &= 15^2 = 225\,,\\[5pt]
 +
\textrm{RHS of (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt]
 +
\textrm{LHS of (3)} &= 39^2 = 1521\,,\\[5pt]
 +
\textrm{RHS of (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.}
 +
\end{align}</math>}}

Current revision

First, let's decide to determine all distance in dm (decimeters), so that we have all the distances as integers.

Call the length of the washing line from the trees to the hanger y and z, as in the figure below, and introduce two auxiliary triangles which have y and z as their hypotenuses. (As an approximation, we suppose that the taut washing line consists of two straight parts.)


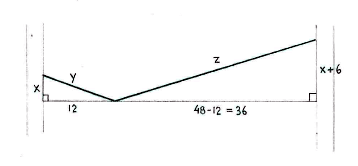
Image:4_1_10-1(5)_.gif


Because the line is 54 dm long, we have

\displaystyle y+z=54\,\textrm{.} (1)

Then, the Pythagorean theorem gives the relations

\displaystyle y^2 = x^2 + 12^2\,, (2)
\displaystyle z^2 = (x+6)^2 + 36^2\,\textrm{.} (3)

The idea now is to solve the system of equations (1)-(3) by first eliminating z, so that we get two equations which only contain x and y. Then, eliminate y from one of these equations, so that we get an equation which determines x.

From (1), we have \displaystyle z = 54-y, and substituting this into (3) gives us the equation

\displaystyle (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} (3')

Equations (2) and (3') together give a smaller system for x and y,

\displaystyle \left\{ \begin{align}

& y^2 = x^2 + 12^2\,,\\[5pt] & (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3')\end{align}

Expand the quadratic terms on both sides of (3'),

\displaystyle 54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,

and simplify

\displaystyle 2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}

Use (2) and replace \displaystyle y^2 with \displaystyle x^2+12 in this equation,

\displaystyle 2916 - 108y + x^2 + 144 = x^2 + 12x + 1332

which gets rid of the x²-term,

\displaystyle 2916 - 108y + 144 = 12x + 1332\,,

and further simplification gives the equation

\displaystyle 12x + 108y = 1728 (3")

If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear

\displaystyle \left\{ \begin{align}

& y^2 = x^2 + 12^2\,,\\[5pt] & 12x+108y=1728\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3")\end{align}

In this system, we can make y the subject in (3"),

\displaystyle y=\frac{1728-12x}{108}=16-\frac{x}{9}

and substitute into (2),

\displaystyle \Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}

This is an equation which only contains x, and if we solve it, we will get our answer.

Expand the quadratic on the left-hand side,

\displaystyle 16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144

and collect together all terms on one side,

\displaystyle x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,

which gives the equation

\displaystyle \frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}

Multiply both sides by \displaystyle 81/80 so that we get the equation in standard form,

\displaystyle x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}

Completing the square on the left-hand side gives

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0

and then

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,

i.e.

\displaystyle x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}

This means that the equation has the solutions

\displaystyle x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}

The answer is thus \displaystyle x=9\ \textrm{dm} (the negative root must be discarded).


To be sure that we have calculated correctly, we also look at the values of y and z, and check that the original equations (1) to (3) are satisfied.

Equation (3") gives

\displaystyle y = 16-\frac{x}{9} = 16-1 = 15

and equation (1) gives

\displaystyle z=54-y=54-15=39\,\textrm{.}

Now, we check that \displaystyle x=9, \displaystyle y=15 and \displaystyle z=39 satisfy the equations (1), (2) and (3),

\displaystyle \begin{align}

\textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt] \textrm{RHS of (1)} &= 54\,,\\[10pt] \textrm{LHS of (2)} &= 15^2 = 225\,,\\[5pt] \textrm{RHS of (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt] \textrm{LHS of (3)} &= 39^2 = 1521\,,\\[5pt] \textrm{RHS of (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.} \end{align}

Retrieved from "http://wiki.sommarmatte.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.1:10"