From Förberedande kurs i matematik 1

Revision as of 11:50, 15 August 2008 (edit) Madde (Talk | contribs) ← Previous diff		Current revision (14:45, 29 September 2008) (edit) (undo) Tek (Talk | contribs)
(5 intermediate revisions not shown.)
Line 1:		Line 1:
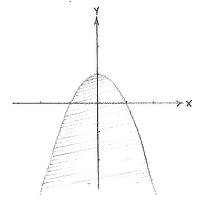
-	{{NAVCONTENT_START}}	+	The inequality <math>y\le 1-x^{2}</math> defines the area under and on the curve
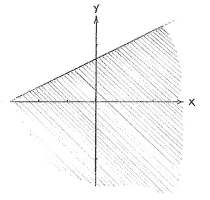
-	<center> [[Bild:2_3_10b-1(3).gif]] </center>	+	<math>y=1-x^{2}</math>, which is a parabola with a maximum at (0,1). We can rewrite the other inequality <math>x\ge 2y-3</math> as <math>y\le x/2+3/2</math> and it defines the area under and on the straight line <math>y=x/2+3/2</math>.
-	{{NAVCONTENT_STOP}}	+
-	{{NAVCONTENT_START}}	+
-	<center> [[Bild:2_3_10b-2(3).gif]] </center>	+	{| align="center"
-	{{NAVCONTENT_STOP}}	+	|align="center"|[[Image:2_3_10_b1-1.gif|center]]
-	{{NAVCONTENT_START}}	+	|width="10px"|&nbsp;
-	<center> [[Bild:2_3_10b-3(3).gif]] </center>	+	|align="center"|[[Image:2_3_10_b1-2.gif|center]]
-	{{NAVCONTENT_STOP}}	+	|-
-	[[Bild:2_3_10_b1.gif|center]]	+	|align="center"|<small>The region y&nbsp;≤&nbsp;1&nbsp;-&nbsp;''x''²</small>
		+	||
		+	|align="center"|<small>The region x&nbsp;≥&nbsp;2''y''&nbsp;-&nbsp;3</small>
		+	|}
		+
		+
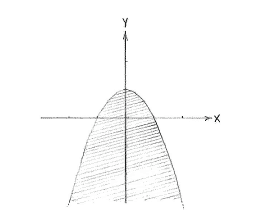
		+	Of the figures above, it seems that the region associated with the parabola lies completely under the line <math>y=x/2+3/2</math> and this means that the area under the parabola satisfies both inequalities.
		+
		+
		+	{| align="center"
		+	|align="center"|[[Image:2_3_10_b2.gif|center]]
		+	|-
		+	|align="center"|<small>The region y&nbsp;≤&nbsp;1&nbsp;-&nbsp;''x''² and x&nbsp;≥&nbsp;2''y''&nbsp;-&nbsp;3</small>
		+	|}
		+
		+
		+	Note: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the ''y''-values on the line <math>y_{\scriptstyle\text{line}} = x/2+3/2</math> is always larger than the corresponding ''y''-value on the parabola <math>y_{\scriptstyle\text{parabola}} = 1-x^{2}</math> by studying the difference between them
		+
		+	{{Displayed math||
		+	<math>y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} = \frac{x}{2} + \frac{3}{2} - (1-x^{2})\,\textrm{.}</math>}}
		+
		+	If this difference is positive regardless of how ''x'' is chosen, then we know that the line's ''y''-value is always greater than the parabola's ''y''-value. After a little simplification and completing the square, we have
		+
		+	{{Displayed math||<math>\begin{align}
		+	y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}}
		+	&= \frac{x}{2} + \frac{3}{2} - (1-x^{2})\\[5pt]
		+	&= x^{2}+\frac{1}{2}x+\frac{1}{2}\\[5pt]
		+	&= \Bigl(x+\frac{1}{4}\Bigr)^{2} - \Bigl(\frac{1}{4}\Bigr)^{2} + \frac{1}{2}\\[5pt]
		+	&= \Bigl(x+\frac{1}{4}\Bigr)^{2} + \frac{7}{16}
		+	\end{align}</math>}}
		+
		+	and this expression is always positive because <math>\tfrac{7}{16}</math> is a positive number and <math>\bigl(x+\tfrac{1}{4}\bigr)^{2}</math> is a quadratic which is never negative. In other words, the parabola is completely under the line.

---

Current revision

The inequality \displaystyle y\le 1-x^{2} defines the area under and on the curve \displaystyle y=1-x^{2}, which is a parabola with a maximum at (0,1). We can rewrite the other inequality \displaystyle x\ge 2y-3 as \displaystyle y\le x/2+3/2 and it defines the area under and on the straight line \displaystyle y=x/2+3/2.

The region y ≤ 1 - x²		The region x ≥ 2y - 3

Of the figures above, it seems that the region associated with the parabola lies completely under the line \displaystyle y=x/2+3/2 and this means that the area under the parabola satisfies both inequalities.

The region y ≤ 1 - x² and x ≥ 2y - 3

Note: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the y-values on the line \displaystyle y_{\scriptstyle\text{line}} = x/2+3/2 is always larger than the corresponding y-value on the parabola \displaystyle y_{\scriptstyle\text{parabola}} = 1-x^{2} by studying the difference between them

\displaystyle y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} = \frac{x}{2} + \frac{3}{2} - (1-x^{2})\,\textrm{.}

If this difference is positive regardless of how x is chosen, then we know that the line's y-value is always greater than the parabola's y-value. After a little simplification and completing the square, we have

\displaystyle \begin{align} y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} &= \frac{x}{2} + \frac{3}{2} - (1-x^{2})\\[5pt] &= x^{2}+\frac{1}{2}x+\frac{1}{2}\\[5pt] &= \Bigl(x+\frac{1}{4}\Bigr)^{2} - \Bigl(\frac{1}{4}\Bigr)^{2} + \frac{1}{2}\\[5pt] &= \Bigl(x+\frac{1}{4}\Bigr)^{2} + \frac{7}{16} \end{align}

and this expression is always positive because \displaystyle \tfrac{7}{16} is a positive number and \displaystyle \bigl(x+\tfrac{1}{4}\bigr)^{2} is a quadratic which is never negative. In other words, the parabola is completely under the line.