From Förberedande kurs i matematik 1

Revision as of 12:29, 3 April 2008 (edit) Oskar (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:4_4_2f.gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (12:44, 13 October 2008) (edit) (undo) Tek (Talk | contribs) m
(4 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	Using the unit circle shows that the equation <math>\cos 3x = -1/\!\sqrt{2}</math>
-	<center> [[Bild:4_4_2f.gif]] </center>	+	has two solutions for <math>0\le 3x\le 2\pi\,</math>,
-	{{NAVCONTENT_STOP}}	+
		+	{{Displayed math||<math>3x = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\qquad\text{and}\qquad 3x = \pi + \frac{\pi}{4} = \frac{5\pi}{4}\,\textrm{.}</math>}}
		+
		+	[[Image:4_4_2_f.gif|center]]
		+
		+	We obtain the other solutions by adding multiples of <math>2\pi</math>,
		+
		+	{{Displayed math||<math>3x = \frac{3\pi}{4} + 2n\pi\qquad\text{and}\qquad 3x = \frac{5\pi}{4} + 2n\pi\,,</math>}}
		+
		+	i.e.
		+
		+	{{Displayed math||<math>x = \frac{\pi}{4} + \frac{2}{3}n\pi\qquad\text{and}\qquad x = \frac{5\pi}{12} + \frac{2}{3}n\pi\,,</math>}}
		+
		+	where ''n'' is an arbitrary integer.

---

Current revision

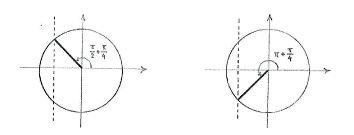
Using the unit circle shows that the equation \displaystyle \cos 3x = -1/\!\sqrt{2} has two solutions for \displaystyle 0\le 3x\le 2\pi\,,

\displaystyle 3x = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\qquad\text{and}\qquad 3x = \pi + \frac{\pi}{4} = \frac{5\pi}{4}\,\textrm{.}

We obtain the other solutions by adding multiples of \displaystyle 2\pi,

\displaystyle 3x = \frac{3\pi}{4} + 2n\pi\qquad\text{and}\qquad 3x = \frac{5\pi}{4} + 2n\pi\,,

i.e.

\displaystyle x = \frac{\pi}{4} + \frac{2}{3}n\pi\qquad\text{and}\qquad x = \frac{5\pi}{12} + \frac{2}{3}n\pi\,,

where n is an arbitrary integer.