From Förberedande kurs i matematik 1

Revision as of 13:29, 2 April 2008 (edit) Oskar (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:4_1_7a-1(2).gif </center> {{NAVCONTENT_STOP}} {{NAVCONTENT_START}} <center> Bild:4_1_7a-2(2).gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (11:19, 8 October 2008) (edit) (undo) Tek (Talk | contribs) m
(3 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	As the equation stands, it is difficult directly to know anything about the circle, but if we complete the square and combine ''x''- and ''y''-terms together in their own respective square terms, then we will have the equation in the standard form
-	<center> [[Bild:4_1_7a-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{{Displayed math||<math>(x-a)^2 + (y-b)^2 = r^2\,,</math>}}
-	{{NAVCONTENT_START}}	+
-	<center> [[Bild:4_1_7a-2(2).gif]] </center>	+	and we will then be able to read off the circle's centre and radius.
-	{{NAVCONTENT_STOP}}	+
		+	If we take the ''x''- and ''y''-terms on the left-hand side and complete the square, we get
		+
		+	{{Displayed math||<math>\begin{align}
		+	x^2 + 2x &= (x+1)^2-1^2\,,\\[5pt]
		+	y^2 - 2y &= (y-1)^2-1^2\,,
		+	\end{align}</math>}}
		+
		+	and then the whole equation can be written as
		+
		+	{{Displayed math||<math>(x+1)^2 - 1^2 + (y-1)^2 - 1^2 = 1\,,</math>}}
		+
		+	or, with the constants moved to the right-hand side,
		+
		+	{{Displayed math||<math>(x+1)^2 + (y-1)^2 = 3\,\textrm{.}</math>}}
		+
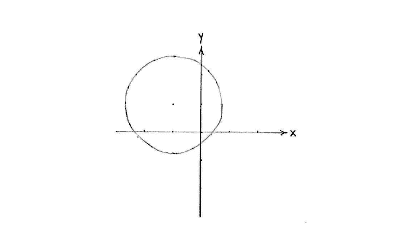
		+	This is a circle having its centre at (-1,1) and radius <math>\sqrt{3}\,</math>.
		+
		+
		+	<center> [[Image:4_1_7a-2(2).gif]] </center>

---

Current revision

As the equation stands, it is difficult directly to know anything about the circle, but if we complete the square and combine x- and y-terms together in their own respective square terms, then we will have the equation in the standard form

\displaystyle (x-a)^2 + (y-b)^2 = r^2\,,

and we will then be able to read off the circle's centre and radius.

If we take the x- and y-terms on the left-hand side and complete the square, we get

\displaystyle \begin{align} x^2 + 2x &= (x+1)^2-1^2\,,\\[5pt] y^2 - 2y &= (y-1)^2-1^2\,, \end{align}

and then the whole equation can be written as

\displaystyle (x+1)^2 - 1^2 + (y-1)^2 - 1^2 = 1\,,

or, with the constants moved to the right-hand side,

\displaystyle (x+1)^2 + (y-1)^2 = 3\,\textrm{.}

This is a circle having its centre at (-1,1) and radius \displaystyle \sqrt{3}\,.