Solution 4.4:7c

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 4.4:7c moved to Solution 4.4:7c: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
If we want to solve the equation
-
<center> [[Image:4_4_7c-1(3).gif]] </center>
+
<math>\text{cos 3}x=\text{sin 4}x</math>, we need an additional result which tells us for which values of
-
{{NAVCONTENT_STOP}}
+
<math>u</math>
-
{{NAVCONTENT_START}}
+
and
-
<center> [[Image:4_4_7c-2(3).gif]] </center>
+
<math>v</math>
-
{{NAVCONTENT_STOP}}
+
the equality
-
{{NAVCONTENT_START}}
+
<math>\text{cos }u=\text{sin }v</math>
-
<center> [[Image:4_4_7c-3(3).gif]] </center>
+
holds, but to get that we have to start with the equality
-
{{NAVCONTENT_STOP}}
+
<math>\cos u=\cos v</math>.
 +
 
 +
So, we start by looking at the equality
 +
 
 +
 
 +
<math>\cos u=\cos v</math>
 +
 
 +
 
 +
We know that for fixed
 +
<math>u</math>
 +
there are two angles
 +
<math>v=u\text{ }</math>
 +
and
 +
<math>v=-\text{u}</math>
 +
in the unit circle which have the cosine value
 +
<math>\cos u</math>, i.e. their
 +
<math>x</math>
 +
-coordinate is equal to
 +
<math>\cos u</math>.
 +
 
[[Image:4_4_7_c1.gif|center]]
[[Image:4_4_7_c1.gif|center]]
 +
 +
Imagine now that the whole unit circle is rotated anti-clockwise an angle
 +
<math>{\pi }/{2}\;</math>. The line
 +
<math>x=\cos u</math>
 +
will become the line
 +
<math>y=\cos u</math>
 +
and the angles
 +
<math>u</math>
 +
and
 +
<math>-u</math>
 +
are rotated to
 +
<math>u+{\pi }/{2}\;</math>
 +
and
 +
<math>-u+{\pi }/{2}\;</math>, respectively.
 +
[[Image:4_4_7_c2.gif|center]]
[[Image:4_4_7_c2.gif|center]]
 +
 +
The angles
 +
<math>u+{\pi }/{2}\;</math>
 +
and
 +
<math>-u+{\pi }/{2}\;</math>
 +
therefore have their
 +
<math>y</math>
 +
-coordinate, and hence sine value, equal to
 +
<math>\cos u</math>. In other words, the equality
 +
 +
 +
<math>\text{cos }u=\text{sin }v</math>
 +
 +
 +
holds for fixed
 +
<math>u</math>
 +
in the unit circle when
 +
<math>v=\pm u+{\pi }/{2}\;</math>, and more generally when
 +
 +
 +
<math>v=\pm u+\frac{\pi }{2}+2n\pi </math>
 +
(
 +
<math>n</math>
 +
an arbitrary integer).
 +
 +
For our equation
 +
<math>\text{cos 3}x=\text{sin 4}x</math>, this result means that
 +
<math>x\text{ }</math>
 +
must satisfy
 +
 +
 +
<math>4x=\pm 3x+\frac{\pi }{2}+2n\pi </math>
 +
 +
 +
This means that the solutions to the equation are
 +
 +
 +
<math>\left\{ \begin{array}{*{35}l}
 +
x=\frac{\pi }{2}+2n\pi \\
 +
x=\frac{\pi }{14}+\frac{2}{7}\pi n \\
 +
\end{array} \right.</math>
 +
(
 +
<math>n</math>
 +
an arbitrary integer)

Revision as of 13:20, 1 October 2008

If we want to solve the equation \displaystyle \text{cos 3}x=\text{sin 4}x, we need an additional result which tells us for which values of \displaystyle u and \displaystyle v the equality \displaystyle \text{cos }u=\text{sin }v holds, but to get that we have to start with the equality \displaystyle \cos u=\cos v.

So, we start by looking at the equality


\displaystyle \cos u=\cos v


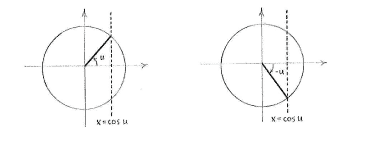
We know that for fixed \displaystyle u there are two angles \displaystyle v=u\text{ } and \displaystyle v=-\text{u} in the unit circle which have the cosine value \displaystyle \cos u, i.e. their \displaystyle x -coordinate is equal to \displaystyle \cos u.


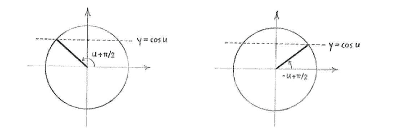
Imagine now that the whole unit circle is rotated anti-clockwise an angle \displaystyle {\pi }/{2}\;. The line \displaystyle x=\cos u will become the line \displaystyle y=\cos u and the angles \displaystyle u and \displaystyle -u are rotated to \displaystyle u+{\pi }/{2}\; and \displaystyle -u+{\pi }/{2}\;, respectively.


The angles \displaystyle u+{\pi }/{2}\; and \displaystyle -u+{\pi }/{2}\; therefore have their \displaystyle y -coordinate, and hence sine value, equal to \displaystyle \cos u. In other words, the equality


\displaystyle \text{cos }u=\text{sin }v


holds for fixed \displaystyle u in the unit circle when \displaystyle v=\pm u+{\pi }/{2}\;, and more generally when


\displaystyle v=\pm u+\frac{\pi }{2}+2n\pi ( \displaystyle n an arbitrary integer).

For our equation \displaystyle \text{cos 3}x=\text{sin 4}x, this result means that \displaystyle x\text{ } must satisfy


\displaystyle 4x=\pm 3x+\frac{\pi }{2}+2n\pi


This means that the solutions to the equation are


\displaystyle \left\{ \begin{array}{*{35}l} x=\frac{\pi }{2}+2n\pi \\ x=\frac{\pi }{14}+\frac{2}{7}\pi n \\ \end{array} \right. ( \displaystyle n an arbitrary integer)

Retrieved from "http://wiki.sommarmatte.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.4:7c"