Solution 2.3:10b
From Förberedande kurs i matematik 1
m |
|||
| Line 1: | Line 1: | ||
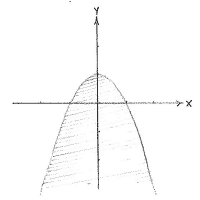
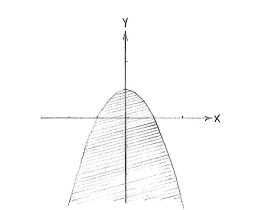
| - | The inequality | + | The inequality <math>y\le 1-x^{2}</math> defines the area under and on the curve |
| - | <math>y\le | + | <math>y=1-x^{2}</math>, which is a parabola with a maximum at (0,1). We can rewrite the other inequality <math>x\ge 2y-3</math> as <math>y\le x/2+3/2</math> and it defines the area under and on the straight line <math>y=x/2+3/2</math>. |
| - | defines the area under and on the curve | + | |
| - | <math>y= | + | |
| - | + | ||
| - | <math>x\ge | + | |
| - | as | + | |
| - | <math>y\le | + | |
| - | and it defines the area under and on the straight line | + | |
| - | <math>y= | + | |
| - | [[Image:2_3_10_b1.gif|center]] | + | {| align="center" |
| - | + | |align="center"|[[Image:2_3_10_b1-1.gif|center]] | |
| - | < | + | |width="10px"| |
| - | + | |align="center"|[[Image:2_3_10_b1-1.gif|center]] | |
| + | |- | ||
| + | |align="center"|<small>The region y ≤ 1 - ''x''²</small> | ||
| + | || | ||
| + | |align="center"|<small>The region x ≥ 2''y'' - 3</small> | ||
| + | |} | ||
| - | [[Image:2_3_10_b2.gif|center]] | ||
| - | + | Of the figures above, it seems that the region associated with the parabola lies completely under the line <math>y=x/2+3/2</math> and this means that the area under the parabola satisfies both inequalities. | |
| - | <math>y | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | {| align="center" | |
| + | |align="center"|[[Image:2_3_10_b2.gif|center]] | ||
| + | |- | ||
| + | |align="center"|<small>The region y ≤ 1 - ''x''² and x ≥ 2''y'' - 3</small> | ||
| + | |} | ||
| - | If | + | Note: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the ''y''-values on the line <math>y_{\scriptstyle\text{line}} = x/2+3/2</math> is always larger than the corresponding ''y''-value on the parabola <math>y_{\scriptstyle\text{parabola}} = 1-x^{2}</math> by studying the difference between them |
| - | + | ||
| - | + | ||
| - | <math> | + | |
| - | + | ||
| - | <math> | + | |
| - | + | ||
| + | {{Displayed math|| | ||
| + | <math>y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} = \frac{x}{2} + \frac{3}{2} - (1-x^{2})\,\textrm{.}</math>}} | ||
| - | + | If this difference is positive regardless of how ''x'' is chosen, then we know that the line's ''y''-value is always greater than the parabola's ''y''-value. After a little simplification and completing the square, we have | |
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\begin{align} | ||
| + | y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} | ||
| + | &= \frac{x}{2} + \frac{3}{2} - (1-x^{2})\\[5pt] | ||
| + | &= x^{2}+\frac{1}{2}x+\frac{1}{2}\\[5pt] | ||
| + | &= \Bigl(x+\frac{1}{4}\Bigr)^{2} - \Bigl(\frac{1}{4}\Bigr)^{2} + \frac{1}{2}\\[5pt] | ||
| + | &= \Bigl(x+\frac{1}{4}\Bigr)^{2} + \frac{7}{16} | ||
| + | \end{align}</math>}} | ||
| - | and this expression is always positive because | + | and this expression is always positive because <math>\tfrac{7}{16}</math> is a positive number and <math>\bigl(x+\tfrac{1}{4}\bigr)^{2}</math> is a quadratic which is never negative. In other words, the parabola is completely under the line. |
| - | <math>\ | + | |
| - | is a positive number and | + | |
| - | <math>\ | + | |
| - | is a quadratic which is never negative. In other words, the parabola is completely under the line. | + | |
Revision as of 14:44, 29 September 2008
The inequality \displaystyle y\le 1-x^{2} defines the area under and on the curve \displaystyle y=1-x^{2}, which is a parabola with a maximum at (0,1). We can rewrite the other inequality \displaystyle x\ge 2y-3 as \displaystyle y\le x/2+3/2 and it defines the area under and on the straight line \displaystyle y=x/2+3/2.
| The region y ≤ 1 - x² | The region x ≥ 2y - 3 |
Of the figures above, it seems that the region associated with the parabola lies completely under the line \displaystyle y=x/2+3/2 and this means that the area under the parabola satisfies both inequalities.
| The region y ≤ 1 - x² and x ≥ 2y - 3 |
Note: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the y-values on the line \displaystyle y_{\scriptstyle\text{line}} = x/2+3/2 is always larger than the corresponding y-value on the parabola \displaystyle y_{\scriptstyle\text{parabola}} = 1-x^{2} by studying the difference between them
|
\displaystyle y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} = \frac{x}{2} + \frac{3}{2} - (1-x^{2})\,\textrm{.} |
If this difference is positive regardless of how x is chosen, then we know that the line's y-value is always greater than the parabola's y-value. After a little simplification and completing the square, we have
| \displaystyle \begin{align}
y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} &= \frac{x}{2} + \frac{3}{2} - (1-x^{2})\\[5pt] &= x^{2}+\frac{1}{2}x+\frac{1}{2}\\[5pt] &= \Bigl(x+\frac{1}{4}\Bigr)^{2} - \Bigl(\frac{1}{4}\Bigr)^{2} + \frac{1}{2}\\[5pt] &= \Bigl(x+\frac{1}{4}\Bigr)^{2} + \frac{7}{16} \end{align} |
and this expression is always positive because \displaystyle \tfrac{7}{16} is a positive number and \displaystyle \bigl(x+\tfrac{1}{4}\bigr)^{2} is a quadratic which is never negative. In other words, the parabola is completely under the line.